早教吧作业答案频道 -->数学-->
如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.(1)求∠CDO的度数;(2)
题目详情
如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.
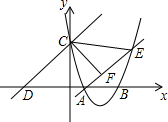
(1)求∠CDO的度数;
(2)求出点F坐标的表达式(用含t的代数式表示);
(3)当S△COD-S四边形COAF=7时,求抛物线解析式;
(4)当以B,C,O三点为顶点的三角形与△CEF相似时,请直接写出t的值.

(1)求∠CDO的度数;
(2)求出点F坐标的表达式(用含t的代数式表示);
(3)当S△COD-S四边形COAF=7时,求抛物线解析式;
(4)当以B,C,O三点为顶点的三角形与△CEF相似时,请直接写出t的值.
▼优质解答
答案和解析
(1)∵直线l:y=x+2t与y轴点C,交x轴于点D,
∴C(0,2t),D(-2t,0)
∴OC=OD,
∵∠COD=90°,
∴∠CDO=∠DCO=45°.
(2)如图1,作FG⊥x轴于点G,FH⊥y轴于点H,
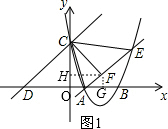
∵∠HOG=∠OGF=∠FHO=90°,
∴四边形OGFH是矩形
∴∠HFG=90°,
∴∠HFA+∠AFG=90°
又∵CF⊥AE,
∴∠CFH+∠HFA=90°
∴∠CFH=∠AFG,
又∵∠CAE=∠CDO=45°,
∴∠FCA=45°,
∴CF=AF,
又∵∠FGA=∠CHF=90°,
在△FGA和△FHC中,
∴△FGA≌△FHC,
∴FH=FG,HC=AG,
设F(m,m)
则2t-m=m-2,
得m=t+1,
∴F(t+1,t+1).
(3)∵S△COD-S四边形COAF=S△COD-S正方形HOGF=7
∴
(2t)2-(t+1)2=7,
解得:t=4或-2(舍去),
则A点坐标(2,0),B点坐标(4,0),C点坐标(0,8)
设y=a(x-2)(x-4),
把C(0,8)代入y=a(x-2)(x-4),
解得a=1,
∴y=(x-2)(x-4)=x2-6x+8.
(4)t=3或2.
如图2,作ET⊥HF于T,
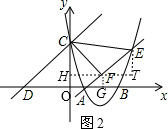
求得:E的横坐标是
,CH=t-1,FT=
,
由△HCF∽△TFE,
则
=
,
得:
=
当△OBC∽△FEC时,
=
=2,
即
=2,
解得:t=3或t=-1( 舍去),
当△OBC∽△FCE时,
=
=
,
即
=
,
解得:t=2或t=0(舍去).
∴t=3或2.
∴C(0,2t),D(-2t,0)
∴OC=OD,
∵∠COD=90°,
∴∠CDO=∠DCO=45°.
(2)如图1,作FG⊥x轴于点G,FH⊥y轴于点H,

∵∠HOG=∠OGF=∠FHO=90°,
∴四边形OGFH是矩形
∴∠HFG=90°,
∴∠HFA+∠AFG=90°
又∵CF⊥AE,
∴∠CFH+∠HFA=90°
∴∠CFH=∠AFG,
又∵∠CAE=∠CDO=45°,
∴∠FCA=45°,
∴CF=AF,
又∵∠FGA=∠CHF=90°,
在△FGA和△FHC中,
|
∴△FGA≌△FHC,
∴FH=FG,HC=AG,
设F(m,m)
则2t-m=m-2,
得m=t+1,
∴F(t+1,t+1).
(3)∵S△COD-S四边形COAF=S△COD-S正方形HOGF=7
∴
| 1 |
| 2 |
解得:t=4或-2(舍去),
则A点坐标(2,0),B点坐标(4,0),C点坐标(0,8)
设y=a(x-2)(x-4),
把C(0,8)代入y=a(x-2)(x-4),
解得a=1,
∴y=(x-2)(x-4)=x2-6x+8.
(4)t=3或2.
如图2,作ET⊥HF于T,

求得:E的横坐标是
| t2+1 |
| t-1 |
| 2 |
| t-1 |
由△HCF∽△TFE,
则
| CH |
| FT |
| CF |
| EF |
得:
| (t-1)2 |
| 2 |
| CF |
| EF |
当△OBC∽△FEC时,
| OC |
| OB |
| CF |
| EF |
即
| (t-1)2 |
| 2 |
解得:t=3或t=-1( 舍去),
当△OBC∽△FCE时,
| OB |
| OC |
| CF |
| EF |
| 1 |
| 2 |
即
| (t-1)2 |
| 2 |
| 1 |
| 2 |
解得:t=2或t=0(舍去).
∴t=3或2.
看了如图,已知抛物线经过点A(2,...的网友还看了以下:
已知P是反比例函数y=x/k(k不等于0)图像上的一点,点P到X轴的距离为3,到Y轴的距离为2,党 2020-05-16 …
已知,点A、B分别是X轴、Y轴上的动点,点C、D是反比例函数y=k/x(k大于0)图像上的点,其中 2020-05-17 …
已知二次函数的图像如图,下列结论正确的是1.a小于b小于02.a+c小于03.4a+c小于已知二次 2020-06-12 …
一次函数当图象与X轴平行时一次函数Y=KX+B(K不等于0)当图象与X轴平行时,斜率K等于多少?( 2020-06-29 …
已知一次函数y=kx+b(k不等于0)图像过点(2,0),且与两坐标轴围成的三角形面积为2,求此一 2020-07-12 …
二次函数y=x^2-|k|与正比例函数y=kx(k不等于0)图像的位置关系为()A.相离B.相切C 2020-07-26 …
二次函数:y=ax^2-bx+b(a大于0,b大于0)图像顶点的纵坐标不大于-b/2.(1)求该二 2020-08-01 …
Y^2-X^2小于等于0图像如何表示? 2020-11-01 …
急!二次函数已知:二次函数y=-1/2x^2-(m+3)x+m^2-12的图象与X轴相交于A(X1, 2020-11-27 …
图象与Y轴的交点关于对称轴的对称点的坐标图象与x轴交点坐标是(-1,0)(-2,0)图象与y轴的交点 2021-01-15 …