早教吧作业答案频道 -->数学-->
已知x,y满足约束条件x+y-2≤0x-2y-2≤02x-y+2≥0,若可行域内存在(x,y)使
题目详情
已知x,y满足约束条件
,若可行域内存在(x,y)使不等式2x+y+k≥0有解,则实数k的取值范围为___.
| |
|
▼优质解答
答案和解析
由约束条件
作出可行域如图,
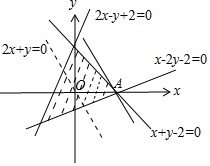
当k≥0时,可行域内存在(x,y)使不等式2x+y+k≥0有解;
当k<0时,要使可行域内存在(x,y)使不等式2x+y+k≥0有解,
则目标函数z=2x+y+k的最大值2×2+0+k≥0,即k≥-4.
综上,可行域内存在(x,y)使不等式2x+y+k≥0有解,实数k的取值范围为[-4,+∞).
故答案为:[-4,+∞).
|

当k≥0时,可行域内存在(x,y)使不等式2x+y+k≥0有解;
当k<0时,要使可行域内存在(x,y)使不等式2x+y+k≥0有解,
则目标函数z=2x+y+k的最大值2×2+0+k≥0,即k≥-4.
综上,可行域内存在(x,y)使不等式2x+y+k≥0有解,实数k的取值范围为[-4,+∞).
故答案为:[-4,+∞).
看了已知x,y满足约束条件x+y-...的网友还看了以下:
下列说法正确的是()①代数式ab+1的意义是a除以b的商与1的和;②要使y=3-xx有意义,则x应 2020-05-14 …
一家小型放映厅的盈利额y同售票数x,其中保险部门规定:超过150人时,要缴纳公安消防保险费50元. 2020-06-02 …
1设z=2y-2x+4,式中x,y满足①0≤x≤1,0≤y≤2,2y-x≥1,求z的最值2在空间直 2020-06-14 …
若对于满足0≤x≤2的一切实数,函数y=(2-k)x-3k+7的值恒大于0,求实数k的取值范围 2020-06-27 …
变上限积分求导f(x)=∫(0,x)(x-t)^2*f(t)dt如何对x求导?原题:函数f(x)满 2020-07-31 …
将函数y=2x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的折线是函数y=| 2020-08-01 …
已知二次函数y=x2-2mx+1.记当x=c时,函数值为yc,那么,是否存在实数m,使得对于满足0 2020-08-01 …
1.已知inti=0,x=1,y=0;在下列选项使i的值变成1的语句是().(A)if(x&&y)i 2020-11-01 …
若同时满足0≤x<1,2<x≤3的值也满足不等式2x^2+mx-1<0,求实数m的取值范围.若满足0 2020-11-19 …
如果函数f(x)满足两个恒等式:f(-x)+f(x)=0,f(x+2)+f(x)=0,又知当0≤x≤ 2020-12-22 …