早教吧作业答案频道 -->数学-->
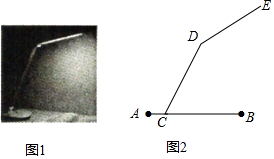
如图1为放置在水平桌面上的某创意可折叠台灯的平面示意图,将其抽象成图2,量的∠DCB=60°,∠CDE=150°,灯杆CD的长为40cm,灯管DE的长为26cm,底座AB的厚度为2cm,不考虑其他因素,分别求出D
题目详情
如图1为放置在水平桌面上的某创意可折叠台灯的平面示意图,将其抽象成图2,量的∠DCB=60°,∠CDE=150°,灯杆CD的长为40cm,灯管DE的长为26cm,底座AB的厚度为2cm,不考虑其他因素,分别求出DE与水平卓,面(AB所在的直线)所成的夹角度数和台灯的高(点E到桌面的距离).(结果保留根号)

▼优质解答
答案和解析
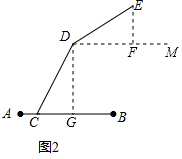 如图,过点D作AB的平行线DM,
如图,过点D作AB的平行线DM,
∵∠DCB=60°,
∴∠CDM=180°-∠DCB=120°,
∵∠CDE=150°,
∴∠EDM=∠CDE-∠CDM=150°-120°=30°,
即DE与水平桌面(AB所在的直线)所成的夹角度数为30°;
作EF⊥DM于点F,DG⊥AB于点G.
∵在直角△DEF中,∠EFD=90°,∠EDF=30°,DE=26cm,
∴EF=
DE=13cm,
∵在直角△CDG中,∠DGC=90°,∠DCG=60°,CD=40cm,
∴sin60°=
,
∴DG=CD•sin60°=40×
=20
cm,
∵底座AB的厚度为2cm,
∴点E到桌面的距离是:13+20
+2=(15+20
)cm.
答:台灯的高(点E到桌面的距离)为(15+20
)cm.
 如图,过点D作AB的平行线DM,
如图,过点D作AB的平行线DM,∵∠DCB=60°,
∴∠CDM=180°-∠DCB=120°,
∵∠CDE=150°,
∴∠EDM=∠CDE-∠CDM=150°-120°=30°,
即DE与水平桌面(AB所在的直线)所成的夹角度数为30°;
作EF⊥DM于点F,DG⊥AB于点G.
∵在直角△DEF中,∠EFD=90°,∠EDF=30°,DE=26cm,
∴EF=
| 1 |
| 2 |
∵在直角△CDG中,∠DGC=90°,∠DCG=60°,CD=40cm,
∴sin60°=
| DG |
| CD |
∴DG=CD•sin60°=40×
| ||
| 2 |
| 3 |
∵底座AB的厚度为2cm,
∴点E到桌面的距离是:13+20
| 3 |
| 3 |
答:台灯的高(点E到桌面的距离)为(15+20
| 3 |
看了如图1为放置在水平桌面上的某创...的网友还看了以下:
1.以知AB=AC,D是AB上一点,DE垂直BC于E,ED的延长线交CA的延长线于F,那么三角形A 2020-04-27 …
(2007•青岛)将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为E 2020-05-15 …
(2011•金衢十一校模拟)如图正方形ABCD,其边长为4.P是射线AB上的点,且AP=x.将△A 2020-06-10 …
各位文言文达人来下有几个而我不知道在句子里起的作用请给位大侠讲下A并列B承接C修饰D转折1.如镜之 2020-06-12 …
ABCD是一张正方形纸片,EF分别为AB,CD的中点,沿过点D的折痕将A角翻折,使得点A落在EF上 2020-06-22 …
正方形ABCD中,A1,A2...An是依次从A到B的n+1等分点,同样Bi是从B到C的n+1等分 2020-06-22 …
如图①,ABCD是一张正方形纸片,E、F分别为AB、CD的中点,沿过点D的折痕将A角翻折,使得点A 2020-07-04 …
《醉翁亭记》“而”的用法:A并列B修饰C顺承D转折1.水深而鱼肥2.水落而石出者3.临溪而渔4.渐 2020-07-08 …
如图,ABCD是一张长方形纸片,且AD=2AB,沿过点D的折痕将A角翻折,使得点A落在BC上(如图 2020-07-22 …
自力更生的更是什么意思百折不挠的折1.断2.损失3.弯曲4.转变方向5折服6.折叠 2020-11-22 …