早教吧作业答案频道 -->数学-->
如图,AE是△ABD的中线AB=CD=BD.(1)求证:AB+AD>2AE;(2)求证:AC=2AE.
题目详情
如图,AE是△ABD的中线AB=CD=BD.
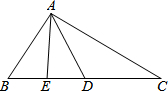
(1)求证:AB+AD>2AE;
(2)求证:AC=2AE.

(1)求证:AB+AD>2AE;
(2)求证:AC=2AE.
▼优质解答
答案和解析
证明:(1)延长AE到M,使AE=EM,连接DM,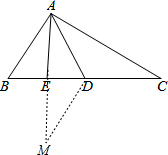
∵AE为△ABD的中线,
∴BE=DE,
在△AEB和△MED中
∴△AEB≌△MED(SAS),
∴AB=DM,
在△AMD中,AD+DM>AM,
即AB+AD>2AE;
(2)∵AE是△ABD的中线,
∴BD=CD,BE=DE,
∴BE=
BD,
∵BD=DC,
∴BD=
BC;
又∵AB=BD,
∴BE=
AB,AB=
BC,
∴
=
=
,
∵∠B=∠B,
∴△ABE∽△CBA,
∴
=
=
,
∴AC=2AE.

∵AE为△ABD的中线,
∴BE=DE,
在△AEB和△MED中
|
∴△AEB≌△MED(SAS),
∴AB=DM,
在△AMD中,AD+DM>AM,
即AB+AD>2AE;
(2)∵AE是△ABD的中线,
∴BD=CD,BE=DE,
∴BE=
| 1 |
| 2 |
∵BD=DC,
∴BD=
| 1 |
| 2 |
又∵AB=BD,
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| BE |
| AB |
| AB |
| BC |
| 1 |
| 2 |
∵∠B=∠B,
∴△ABE∽△CBA,
∴
| AE |
| AC |
| BE |
| AB |
| 1 |
| 2 |
∴AC=2AE.
看了如图,AE是△ABD的中线AB...的网友还看了以下:
数学证明题如图,AD=16,AB=15,BC=16,CD=15,求证:四边形ABCD是平行四边形. 2020-05-01 …
如图,▱ABCD的对角线相交于点O,将线段OD绕点O旋转,使点D的对应点落在BC延长线上的点E处, 2020-05-12 …
一道初三圆的题如下图,已知,AB、CD是⊙O的两条弦,AB=CD,且AB⊥CD,垂足为E,OF⊥A 2020-05-13 …
如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF. (1 2020-05-17 …
1.在梯形ABCD中AB‖CD(CD是上底,AB是下底),∠A+∠B=90°,E和F分别为AB和C 2020-05-22 …
(1/3)(1)点C是AB的中点,CD平行BE,且CD=BE,求证:角D=角E.(2)小玉用四根木 2020-06-02 …
BD CD是三角形ABC的外交,角CBE与角BCF的角平分线BD和CD交于点D 证明BD CD是三 2020-06-27 …
如图,已知BE是△ABC的外接圆⊙○直径,CD是△ABC的高.求证:AC×BC=BE×CD:已知C 2020-06-27 …
用反证法证明命题:“如图,如果AB//CD,AB//EF,那么CD//EF”,证明的第一个步骤是( 2020-08-01 …
用反证法证明命题:如果AB⊥CD,AB⊥EF,那么CD∥EF,证明的第一个步骤是()A.假设CD∥ 2020-08-01 …