早教吧作业答案频道 -->数学-->
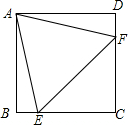
如图,在正方形ABCD中,E为BC边上的点(不与B,C重合),F为CD边上的点(不与C,D重合),且AE=AF,AB=4,设△AEF的面积为y,EC的长为x,求y关于x的函数关系式,并写出自变量x的取值范围.
题目详情
如图,在正方形ABCD中,E为BC边上的点(不与B,C重合),F为CD边上的点(不与C,D重合),且AE=AF,AB=4,设△AEF的面积为y,EC的长为x,求y关于x的函数关系式,并写出自变量x的取值范围.

▼优质解答
答案和解析
∵在正方形ABCD中,
∴AB=AD,
∵AE=AF,
∴在Rt△ABF和Rt△ADE中
∵
,
∴Rt△ABF≌Rt△ADE(HL),
∴BF=DE,
∵EC的长为x,
∴FC=x,BF=4-x,DE=4-x,
∴△AEF的面积为:
y=16-S△ABF-S△ADE-S△EFC
=16-
×4(4-x)-
×4(4-x)-
x2
=-
x2+4x(0<x<4).
∴AB=AD,
∵AE=AF,
∴在Rt△ABF和Rt△ADE中
∵
|
∴Rt△ABF≌Rt△ADE(HL),
∴BF=DE,
∵EC的长为x,
∴FC=x,BF=4-x,DE=4-x,
∴△AEF的面积为:
y=16-S△ABF-S△ADE-S△EFC
=16-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
看了如图,在正方形ABCD中,E为...的网友还看了以下:
大学数学概率独立性的问题盒中有编号为1.2.3.4的4个球,随机地自盒中取一只球,事件A为“取得的 2020-04-06 …
设直线l的方程是2x+By-1=0,倾斜角为α.(1)试将α表示为B的函数;(2)若π6<α<2π 2020-04-11 …
概率题急求解1设A,B为随机事件且P(A)=0.7,P(A-B)=0.3,求P(A非B非).2设A 2020-04-12 …
已知两个非零向量a,b,且向量a与向量b平行,……(如下)已知两个非零向量a,b,且向量a与向量b 2020-05-15 …
已知向量A 向量B是不平行的非零向量 t属于R 则当(向量a+t向量b)的模取最小值时 向量B 与 2020-05-15 …
如图,有足够多的边长为a的小正方形、边长为b的大正方形以及长为a宽为b的长方形(1)、取其中若干个 2020-05-16 …
EXecl表格的一列中值为A的为B的为C的怎么用函数把它们加一起求和 2020-05-17 …
有A,B,C三类产品做质量检查,取到A类产品的概率为0.9,取到B类产品的概率是0.05,取到C类 2020-05-19 …
从1234567中任取3个不同的数,事件A为:取到的3个数和为奇数.事件B为:取到的3个数均为奇数 2020-05-21 …
根据报道美国人血型的分布近似地为:A型为37%,O型为44%,B型为13%,AB型为6%.夫妻拥有 2020-05-22 …