早教吧作业答案频道 -->数学-->
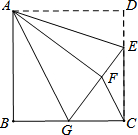
如图,正方形ABCD中,点E在边CD上,且CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.求证:(1)△ABG≌△AFG;(2)AG∥CF.
题目详情
如图,正方形ABCD中,点E在边CD上,且CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
求证:(1)△ABG≌△AFG;
(2)AG∥CF.
求证:(1)△ABG≌△AFG;
(2)AG∥CF.

▼优质解答
答案和解析
证明:(1)∵四边形ABCD是正方形,
∴AB=AD=DC=6,∠B=D=90°,
∵CD=3DE,
∴DE=2,
∵△ADE沿AE折叠得到△AFE,
∴DE=EF=2,AD=AF,∠D=∠AFE=∠AFG=90°,
∴AF=AB,
在Rt△ABG和Rt△AFG中,
,
∴Rt△ABG≌Rt△AFG(HL);
(2)∵Rt△ABG≌Rt△AFG,
∴BG=FG,∠AGB=∠AGF,
设正方形ABCD的边长为6,BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2,
在Rt△ECG中,由勾股定理得:CG2+CE2=EG2,
∵CG=6-x,CE=4,EG=x+2
∴(6-x)2+42=(x+2)2
解得:x=3,
∴BG=GF=CG=3,
∴∠CFG=∠FCG,
∵∠BGF=∠CFG+∠FCG,
又∵∠BGF=∠AGB+∠AGF,
∴∠CFG+∠FCG=∠AGB+∠AGF,
∵∠AGB=∠AGF,∠CFG=∠FCG,
∴∠AGB=∠FCG,
∴AG∥CF.
∴AB=AD=DC=6,∠B=D=90°,
∵CD=3DE,
∴DE=2,
∵△ADE沿AE折叠得到△AFE,
∴DE=EF=2,AD=AF,∠D=∠AFE=∠AFG=90°,
∴AF=AB,
在Rt△ABG和Rt△AFG中,
|
∴Rt△ABG≌Rt△AFG(HL);
(2)∵Rt△ABG≌Rt△AFG,
∴BG=FG,∠AGB=∠AGF,
设正方形ABCD的边长为6,BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2,
在Rt△ECG中,由勾股定理得:CG2+CE2=EG2,
∵CG=6-x,CE=4,EG=x+2
∴(6-x)2+42=(x+2)2
解得:x=3,
∴BG=GF=CG=3,
∴∠CFG=∠FCG,
∵∠BGF=∠CFG+∠FCG,
又∵∠BGF=∠AGB+∠AGF,
∴∠CFG+∠FCG=∠AGB+∠AGF,
∵∠AGB=∠AGF,∠CFG=∠FCG,
∴∠AGB=∠FCG,
∴AG∥CF.
看了如图,正方形ABCD中,点E在...的网友还看了以下:
有理数a,b在数轴上的位置如图所示,则a+b的值()A.大于0B.小于0C.等于0D.小于a 2020-05-13 …
食堂每天用大米a千克,用了2天后还剩下b千克,原有大米()千克.A.a+2-bB.2a-bC.2a 2020-05-17 …
图5中abcd四点间存在热力环流,根据四点气压数值判断下列说法正确的是A.由于a处气压低于c处,所 2020-06-12 …
设0<b<1+a,若关于x的不等式(ax)2<(x-b)2的解中恰有四个整数,则a的取值范围是() 2020-06-27 …
读我国某区域示意图,回答1-3题。1.关于A~E省级行政区的简称,对应正确的是[]A.A→甘或陇、 2020-07-11 …
如果关于x的方程x2-ax+a2-3=0至少有一个正根,则实数a的取值范围是()A.-2<a<2B 2020-07-12 …
已知集合A={1,2,3,…,2n}.对于A的一个子集S,若存在不大于n的正整数m,使得对于S中的 2020-07-20 …
如果不等式组(a≠b)无解,那么不等式组的解集是[]A.2-b<x<2-aB.b-2<x<a-2C 2020-07-31 …
2(a-b)3-(b-a)2分解因式正确的是()A.(a-b)2(2a-2b+1)B.2(a-b) 2020-08-03 …
因式分解-2a2+8ab-8b2结果正确的是()A.-2(a2-4ab+4b2)B.-2(a-2b 2020-08-03 …