已知，如图1，正方形ABCD和正方形BEFG，三点A、B、E在同一直线上，连接AG和CE，（1）试确定线段AG和线段CE有什么关系？并说明理由．（2）将正方形BEFG绕点B顺时针旋转到图2的位置时，（1）

Question

已知，如图1，正方形ABCD和正方形BEFG，三点A、B、E在同一直线上，连接AG和CE，
（1）试确定线段 AG和线段CE有什么关系？并说明理由．
（2）将正方形BEFG绕点B顺时针旋转到图2的位置时，（1）中的结论是否还成立？请说明理由．
（3）若在图2中连接AE和CG，且AE=7，CG=3，求正方形ABCD和正方形BEFG的面积之和．

Answer 1

（1）AG=CE，且AG⊥CE．理由如下：
延长AG交CE于H，如图1所示：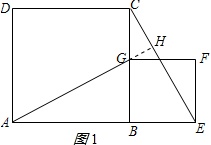
∵四边形ABCD和四边形BEFG是正方形，
∴AB=CB，BG=BE，∠ABG=∠CBE=90°，
在△ABG和△CBE中，

AB=CB	amp;
∠ABG=∠CBE	amp;
BG=BE	amp;

，
∴△ABG≌△CBE（SAS），
∴AG=CE，∠BAG=∠BCE，
∵∠BCE+∠BEC=90°，
∴∠BAG+∠BEC=90°，
∴∠AHE=90°，
∴AG⊥CE；
（2）AG=CE，且AG⊥CE仍然成立．理由如下：
如图2所示：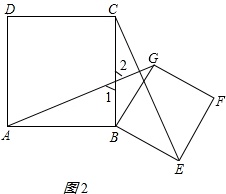
∵四边形ABCD和四边形BEFG是正方形，
∴AB=CB，BG=BE，∠ABC=∠EBG=90°，
∵∠ABG=∠ABC+∠CBG，∠CBE=∠EBG+∠CBG，
∴∠ABG=∠CBE，
在△ABG和△CBE中，

AB=CB	amp;
∠ABG=∠CBE	amp;
BG=BE	amp;

，
∴△ABG≌△CBE（SAS），
∴AG=CE，∠BAG=∠BCE，
∵∠1+∠BAG=90°，
∴∠1+∠BCE=90°，
∵∠1=∠2，
∴∠2+∠BCE=90°，
∴∠AHC=90°，
∴AG⊥CE；
（3）连接AC、EG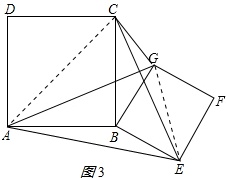，如图3所示：
由（2）得：AG⊥CE，
在Rt△CGH中，CG²=CH²+GH²，
在Rt△AEH中，AE²=AH²+EH²，
∴CG²+AE²=CH²+GH²+AH²+EH²=（CH²+AH²）+（GH²+EH²）=AC²+EG²，
∵AE=7，CG=3，
∴AC²+EG²=3²+7²=58，
∴正方形ABCD和正方形BEFG的面积之和=AB²+BE²=(1)/(2)（AC²+EG²）=(1)/(2)×58=29．