早教吧作业答案频道 -->数学-->
如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.(1)求∠CBD的度数;(2)当点P运动时,∠APB与∠ADB之间的数量关
题目详情
如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
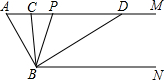
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是___.
▼优质解答
答案和解析
(1)∵AM∥BN,
∴∠A+∠ABN=180°,
∵∠A=60°,
∴∠ABN=120°,
∵BC、BD分别平分∠ABP和∠PBN,
∴∠CBP=
∠ABP,∠DBP=
∠NBP,
∴∠CBD=
∠ABN=60°;

(2)不变化,∠APB=2∠ADB,
证明:∵AM∥BN,
∴∠APB=∠PBN,
∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB=2∠ADB;
(3)∵AD∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠DBN,
由(1)可得,∠CBD=60°,∠ABN=120°,
∴∠ABC=
(120°-60°)=30°,
故答案为:30°.
∴∠A+∠ABN=180°,
∵∠A=60°,
∴∠ABN=120°,
∵BC、BD分别平分∠ABP和∠PBN,
∴∠CBP=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CBD=
| 1 |
| 2 |

(2)不变化,∠APB=2∠ADB,
证明:∵AM∥BN,
∴∠APB=∠PBN,
∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB=2∠ADB;
(3)∵AD∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠DBN,
由(1)可得,∠CBD=60°,∠ABN=120°,
∴∠ABC=
| 1 |
| 2 |
故答案为:30°.
看了如图,已知AM∥BN,∠A=6...的网友还看了以下:
已知圆O半径为5,圆内P一点OP=4,试过P作一条切线,使这条切线=8请用初中方法,可用道具有圆规 2020-06-05 …
函数在某点的左右导数相等,但左右导数值不等于函数这一点的导数值能举一个实例吗?另外,函数在某一点的 2020-06-10 …
三个数的平均数是25.25其中一个数是十二点五,第二个数是第一个数的一点五倍,第三个数是多少? 2020-06-12 …
造句,九个中选7~8个,有点创意,字数多一点面颊、融化、喷嚏、分辨、嘈杂、唠唠叨叨、无动于衷、充耳 2020-06-21 …
把一个一次函数绕一点旋转以后,解析式怎么求!比如函数的图象能由一次函数y=3x﹣2的图象绕点(0, 2020-06-25 …
若函数在一点出可导,推不出导函数在该点邻域内连续,那么有没有在该点邻域内可导的结论呢?可导一定连续 2020-07-31 …
函数在一点连续,那么它的导函数在这一点可能可导吗?我有点懵了,证明函数在一点处可导是要求函数在这一 2020-07-31 …
数学的一个概念不理解多元函数的偏导数在一点连续是指:偏导数在该点的某个邻域内存在,于是偏导数在这邻 2020-07-31 …
有关极限连续可导的问题下面说法是否正确?怎么改正?1若函数在一点处无定义,则函数在该点不连续,不可导 2020-11-03 …
函数在一点的导数不存在,它在这点的左右导数不存在.还有定义“如果函数在一点的左右导数存在到不相等,它 2020-11-25 …