早教吧作业答案频道 -->数学-->
如图,在正方形ABCD中,点P是BC边上一点(不与B、C重合),连接PA,将线段PA绕点P顺时针旋转90°得到线段PE,交边DC于F,连接AE,CE.(1)求证:△ABP∽△PCF;(2)求∠ECF的度数;(3)若∠
题目详情
如图,在正方形ABCD中,点P是BC边上一点(不与B、C重合),连接PA,将线段PA绕点P顺时针旋转90°得到线段PE,交边DC于F,连接AE,CE.
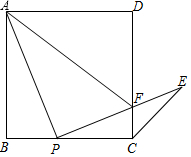
(1)求证:△ABP∽△PCF;
(2)求∠ECF的度数;
(3)若∠APB=75°,PC=2,求S△APE.

(1)求证:△ABP∽△PCF;
(2)求∠ECF的度数;
(3)若∠APB=75°,PC=2,求S△APE.
▼优质解答
答案和解析
 (1)∵四边形ABCD是正方形,
(1)∵四边形ABCD是正方形,
∴AB=BC,∠B=∠PCD=90°,
∴∠PAB+∠APB=90°,
∵∠APE=90°,
∴∠EPC+∠APB=90°,
∴∠PAB=∠EPC,
∴△ABP∽△PCF;
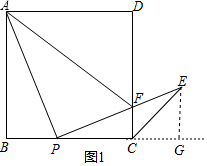
(2)如图1,过点E作EG⊥BC,垂足为G.
在△ABP和△PGE中,
.
∴△ABP≌△PGE,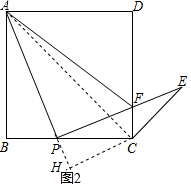
∴BP=EG,PG=AB,
∵AB=BC,
∴BC=PG,
∴BC-PC=PG-PC,即BP=CG,
∴CG=EG,
又∵∠EGC=90°,
∴∠ECG=45°,
∴∠ECF=45°;
(3)如图2,连接AC,过C作CH⊥AP交AP的延长线于H,
设PB=x,则AB=BC=x+2,
∴AC=
(x+2),
∵∠BAP=15°,∠BAC=45°,
∴∠PAC=30°,
∴CH=
AC=
,
∵∠B=∠H=90°,∠APB=∠CPH,
∴△ABP∽△CHP,
∴
=
,即
=
,
∴AP=2
,
∴S△APE=
×2
×2
=4.
 (1)∵四边形ABCD是正方形,
(1)∵四边形ABCD是正方形,∴AB=BC,∠B=∠PCD=90°,
∴∠PAB+∠APB=90°,
∵∠APE=90°,
∴∠EPC+∠APB=90°,
∴∠PAB=∠EPC,
∴△ABP∽△PCF;
(2)如图1,过点E作EG⊥BC,垂足为G.
在△ABP和△PGE中,
|
∴△ABP≌△PGE,

∴BP=EG,PG=AB,
∵AB=BC,
∴BC=PG,
∴BC-PC=PG-PC,即BP=CG,
∴CG=EG,
又∵∠EGC=90°,
∴∠ECG=45°,
∴∠ECF=45°;
(3)如图2,连接AC,过C作CH⊥AP交AP的延长线于H,
设PB=x,则AB=BC=x+2,
∴AC=
| 2 |
∵∠BAP=15°,∠BAC=45°,
∴∠PAC=30°,
∴CH=
| 1 |
| 2 |
| ||
| 2 |
∵∠B=∠H=90°,∠APB=∠CPH,
∴△ABP∽△CHP,
∴
| CH |
| AB |
| PC |
| AP |
| ||||
| x+2 |
| 2 |
| AP |
∴AP=2
| 2 |
∴S△APE=
| 1 |
| 2 |
| 2 |
| 2 |
看了如图,在正方形ABCD中,点P...的网友还看了以下:
1.a≠0,b≠0,则a/|a|+b/|b|的不同取值的个数为()A.3B.2C.1D.02.若|x 2020-03-31 …
基本不等式超费解130已知a>b>0,求a2+1/(a*b)+1/[a*(a-b)]的最小值.a2 2020-05-13 …
1.圆(x-4)^2+(y-4)^2=4与直线y=mx的交点为P.Q,则|OP||OQ|的值为() 2020-05-15 …
设集合A={1,a,b},B={a,a^2,ab}且A=B,求实数A,B的值因为集合需要满足互异性 2020-05-15 …
已知直线方程为(a+3)x(2a-1)y+7=0(1)证明不论a为何实数,直线恒过定点(1)证明不 2020-05-16 …
在“探究加速度与力、质量的关系”这一实验中,有两位同学通过测量,分别作出a一F图象,如图(a)、( 2020-05-17 …
已知直线l:5ax-5y-a+3=0.(1)证明:不论a为何值,直线l总经过第一象限;(2)若直线 2020-06-24 …
假设集合A满足以下条件:诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …
现在有五个命题:①两条直线的位置关系只有相交、平行两种;②过直线外一点可以有多条不同直线与已知直线 2020-08-02 …
在直二面角中,直线直线与斜交,则().A.a不和b垂直,但可能a∥bB.a可能和b垂直,也可能a∥ 2020-08-02 …