早教吧作业答案频道 -->数学-->
在Rt△ABC中,∠ACB=90°,∠BAC=α,分别以AB,CA为底边向△ABC外作等腰三角形ABR和等腰三角形CAQ,连接RQ交AB于点T.(1)当α=45°,△ABR和△CAQ都是等腰直角三角形时,RTTQ
题目详情
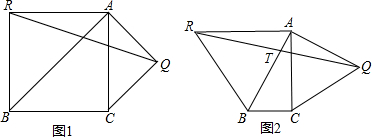
在Rt△ABC中,∠ACB=90°,∠BAC=α,分别以AB,CA为底边向△ABC外作等腰三角形ABR和等腰三角形CAQ,连接RQ交AB于点T.
(1)当α=45°,△ABR和△CAQ都是等腰直角三角形时,
=___.
(2)当α=30°,△ABR和△CAQ都是等边三角形时,求
的值.
(3)当△ABR和△CAQ的底角都是90°-α,tanα=m,直接写出
的值.
(1)当α=45°,△ABR和△CAQ都是等腰直角三角形时,
| RT |
| TQ |
(2)当α=30°,△ABR和△CAQ都是等边三角形时,求
| RT |
| TQ |
(3)当△ABR和△CAQ的底角都是90°-α,tanα=m,直接写出
| RT |
| TQ |

▼优质解答
答案和解析
(1)如图1中,过点Q作QH⊥AC于H,延长交AB于G,连接RG,
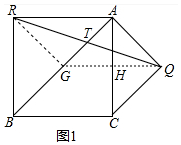
∵AQ=QC,
∴AH=CH,QH⊥AC,
∵∠BCA=90°=∠AHG,
∴GH∥BC,
∴AG=BG,
∵AR=BR,
∴RG⊥AB,
∵∠BAC=∠RAB=∠QAC=45°,
∴∠RAC=∠QAB=90°
∴AD⊥AC,AE⊥AB,
∴GQ∥AR,RG∥AQ,
∴四边形ARGQ是平行四边形,
∴RT=TQ,
∴
=1.
故答案为1.
(2)如图2中,如图1中,过点Q作QH⊥AC于H,延长交AB于G,连接RG,
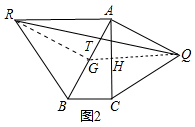
∵AQ=QC,
∴AH=CH,QH⊥AC,
∵∠BCA=90°=∠AHG,
∴GH∥BC,
∴AG=BG,
∵AR=BR,
∴RG⊥AB,
∵∠BAC=30°,∠RAB=∠QAC=60°,
∴∠RAC=∠QAB=90°
∴AD⊥AC,AE⊥AB,
∴GQ∥AR,RG∥AQ,
∴四边形ARGQ是平行四边形,
∴RT=TQ,
∴
=1.
(3)如图3中,如图1中,过点Q作QH⊥AC于H,延长交AB于G,连接RG,
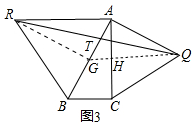
∵AQ=QC,
∴AH=CH,QH⊥AC,
∵∠BCA=90°=∠AHG,
∴GH∥BC,
∴AG=BG,
∵AR=BR,
∴RG⊥AB,
∵∠BAC=α,∠RAB=∠QAC=90°-α,
∴∠RAC=∠QAB=90°
∴AD⊥AC,AE⊥AB,
∴GQ∥AR,RG∥AQ,
∴四边形ARGQ是平行四边形,
∴RT=TQ,
∴
=1.

∵AQ=QC,
∴AH=CH,QH⊥AC,
∵∠BCA=90°=∠AHG,
∴GH∥BC,
∴AG=BG,
∵AR=BR,
∴RG⊥AB,
∵∠BAC=∠RAB=∠QAC=45°,
∴∠RAC=∠QAB=90°
∴AD⊥AC,AE⊥AB,
∴GQ∥AR,RG∥AQ,
∴四边形ARGQ是平行四边形,
∴RT=TQ,
∴
| RT |
| TQ |
故答案为1.
(2)如图2中,如图1中,过点Q作QH⊥AC于H,延长交AB于G,连接RG,

∵AQ=QC,
∴AH=CH,QH⊥AC,
∵∠BCA=90°=∠AHG,
∴GH∥BC,
∴AG=BG,
∵AR=BR,
∴RG⊥AB,
∵∠BAC=30°,∠RAB=∠QAC=60°,
∴∠RAC=∠QAB=90°
∴AD⊥AC,AE⊥AB,
∴GQ∥AR,RG∥AQ,
∴四边形ARGQ是平行四边形,
∴RT=TQ,
∴
| RT |
| TQ |
(3)如图3中,如图1中,过点Q作QH⊥AC于H,延长交AB于G,连接RG,

∵AQ=QC,
∴AH=CH,QH⊥AC,
∵∠BCA=90°=∠AHG,
∴GH∥BC,
∴AG=BG,
∵AR=BR,
∴RG⊥AB,
∵∠BAC=α,∠RAB=∠QAC=90°-α,
∴∠RAC=∠QAB=90°
∴AD⊥AC,AE⊥AB,
∴GQ∥AR,RG∥AQ,
∴四边形ARGQ是平行四边形,
∴RT=TQ,
∴
| RT |
| TQ |
看了在Rt△ABC中,∠ACB=9...的网友还看了以下:
气垫船在水上行驶的速度很快,它所利用的减小水对船的阻力的主要方法是()A.把船底做得很光滑B.在船 2020-05-02 …
(2012•江南区二模)气垫船在水上行驶的速度很快,它所利用的减小水对船的阻力的主要方法是()A. 2020-05-02 …
如图所示,厚底圆柱形容器A、B置于水平桌面中间.A底厚为2h,B底厚为h,容器中液面到水平桌面的高 2020-06-19 …
如图,圆柱的高为10cm,底面半径为2cm.在下底面的A点处有一只蚂蚁,它想吃到上底面上与A点相对 2020-06-27 …
图是一种牲畜饮水用自动装置的示意图.水箱底部有一出水孔,底盖A甲时顶住水箱的出水孔.一旦饮水槽水位 2020-06-30 …
如图(a)所示,轻质薄壁圆柱形容器甲置于水平地面,容器高0.2米,内盛0.15米深的水,水对容器底 2020-07-17 …
下面关于式子(-3)4的几个说法中,正确的是()A.(-3)是底数,4是幂B.3是底数,4是幂C. 2020-07-30 …
同底数幂的除法法则:am÷an=(a≠0,m,n都是正整数,并且m>n).即同底数幂相除,底数,指 2020-07-30 …
下面关于式子(-3)4的几个说法中,正确的是()A.(-3)是底数,4是幂B.3是底数,4是幂C. 2020-08-01 …
(2012•滁州模拟)一个等腰梯形,上底是a分米,下底是b分米,高h分米.沿着底边上的高把它分成两部 2020-11-12 …