早教吧作业答案频道 -->数学-->
为了美化环境,学校准备在如图所示的矩形ABCD空地上迸行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ.已知BC=24米,AB=40米,设AN=x米,种花的面
题目详情
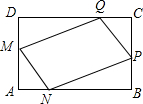
为了美化环境,学校准备在如图所示的矩形ABCD空地上迸行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ.已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.
(1)分别求y1和y2与x之间的函数关系式(不要求写出自变量的取值范围)
(2)当AN的长为多少米时种花的面积为440平方米?
(3)若种花每平方米需200元,铺设草坪每平方米需100元现设计要求种花的面积不大于440平方米,那么学校至少需要准备多少元费用.

(1)分别求y1和y2与x之间的函数关系式(不要求写出自变量的取值范围)
(2)当AN的长为多少米时种花的面积为440平方米?
(3)若种花每平方米需200元,铺设草坪每平方米需100元现设计要求种花的面积不大于440平方米,那么学校至少需要准备多少元费用.
▼优质解答
答案和解析
(1)根据题意,y2=2×
•x•x+2×
(40-x)(24-x)=2x2-64x+960,
y1=40×24-y2=-2x2+64x;
(2)根据题意,知y1=440,即-2x2+64x=440,
解得:x1=10,x2=22,
故当AN的长为10米或22米时种花的面积为440平方米;
(3)设总费用为W元,
则W=200(-2x2+64x)+100(2x2-64x+960)=-200(x-16)2+147200,
由(2)知当0<x≤10或22≤x≤24时,y1≤440,
在W=-200(x-16)2+147200中,当x<16时,W随x的增大而增大,当x>16时,W随x的增大而减小,
∴当x=10时,W取得最大值,最大值W=140000,
当x=22时,W取得最大值,最大值W=140000,
∴学校至少要准备140000元.
| 1 |
| 2 |
| 1 |
| 2 |
y1=40×24-y2=-2x2+64x;
(2)根据题意,知y1=440,即-2x2+64x=440,
解得:x1=10,x2=22,
故当AN的长为10米或22米时种花的面积为440平方米;
(3)设总费用为W元,
则W=200(-2x2+64x)+100(2x2-64x+960)=-200(x-16)2+147200,
由(2)知当0<x≤10或22≤x≤24时,y1≤440,
在W=-200(x-16)2+147200中,当x<16时,W随x的增大而增大,当x>16时,W随x的增大而减小,
∴当x=10时,W取得最大值,最大值W=140000,
当x=22时,W取得最大值,最大值W=140000,
∴学校至少要准备140000元.
看了为了美化环境,学校准备在如图所...的网友还看了以下:
化学公式:c=1000pw/M怎么推出来的?化学公式:c=1000pw/M怎么推出来的?c是物质的 2020-04-08 …
实验室可以按如图所示的装置干燥、贮存气体M,多余的气体可用水吸收,则M是()A.氨气B.一氧化碳C 2020-05-12 …
(1)如果3x-2/x+1=3+m/x+1则m=-5(2) 如果5x-3/x+2=5+m/x+2则 2020-05-16 …
化学方程式M(P)+N(V)=可逆符号C(q)+Z(g)状态都是气体,为什么M+N不等于C+Z时. 2020-05-20 …
在A、B、C、D、E、M、N等物质中,通常情况下,A是具有还原性的单质,B、C、M是无色气体,E是 2020-06-23 …
如何确定一个关系模式的规范化程度F={B->C,(M,T)->B,(M,C)->T,(M,A)-> 2020-06-28 …
如图所示,用石墨作电极电解氯化铜溶液,下列说法正确的是()A.M极是正极B.溶液中的阴离子向N极移动 2020-11-01 …
化学平衡中的气、液、固三系是否分开讨论…?比如,mA(g)+nB(l)=pC(g)+qD(l)+rE 2020-11-03 …
知道一个根,如何把一元三次方程因式分解?像f(x)=4x^3-12x^2+20x-12.知道它的一个 2021-02-05 …
三分子一氧化碳与一分子二氧化硫反应生成两分子二氧化碳和什么中考的一条推断题里有,原来是3X+C=2Y 2021-02-17 …