在实验室中进行了两类细菌竞争食物的实验。在两类细菌的混合培养液中测定了第Ⅰ类细菌后一代(即Zt+1)所占总数的百分数与前一代(即Zt)所占百分数
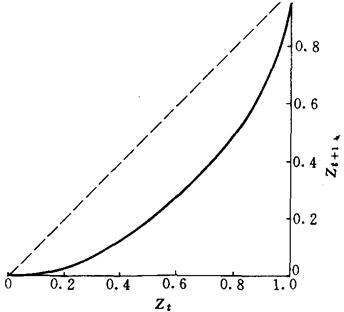
在实验室中进行了两类细菌竞争食物的实验。在两类细菌的混合培养液中测定了第Ⅰ类细菌后一代(即Z t +1 )所占总数的百分数与前一代(即Z t )所占百分数之间的关系。在下图中,实线表示观测到的Z t +1 和Z t 之间的关系,虚线表示Z t +1 =Z t 时的情况。从长远看,第Ⅰ类和第Ⅱ类细菌将会发生什么情况?
A 第Ⅰ类细菌与第Ⅱ类细菌共存
B 两类细菌共同增长
C 第Ⅰ类细菌把第Ⅱ类细菌从混合培养液中排除掉
D 第Ⅱ类细菌把第Ⅰ类细菌从混合培养液中排除掉
D
解析:D正确:因为从上图看,第Ⅰ类细菌后一代在细菌总数中所占的比例总是比前一代少,长此下去,第Ⅰ类细菌所占的比例就会越来越少,直至从混合培养液中消失,即完全被第刀类细菌所排除。A不对:因为第Ⅰ类细菌越来越少,不可能与第Ⅱ类细菌实现长期共存。B不对:因为只有第Ⅱ类细菌在逐渐增长,而第Ⅰ类细菌的相对数量越来越少,直至消失。C不对:因为事实刚好相反。
关于x的方程3tx^2+(3-7t)x+4=0的两个实数根a,b满足0<a<1<b小于2,求t的取 2020-05-16 …
若t是非负数,且关于x的方程(1-t的平方)x的平方+2(1-t)x=0有两个实数根,求t值及对应 2020-05-16 …
关于X的一元二次方程2X^2-tx-2=0有两个实根α、β ,设f(x)关于x的一元二次方程2x^ 2020-05-16 …
已知关于x的一元二次方程x^2-(t-2)x+t^2+3t+5=0已知关于x的方程x^2-(t-2 2020-06-02 …
t(x的平方)+(t+2)x+1=0有两个实根α,β,且满足α1,则实数t的取值范围是 2020-07-19 …
已知函数f(x)=x^2+ax+b-2,其中x=t+1/t.已知函数f(x)=x^2+ax+b-2 2020-07-21 …
11(2)若实数x,y满足:x/(2^10+5^3)+y/(2^10+6^3)=1,x/(3^10 2020-07-22 …
对于二次函数C:y=x2-4x+6和一次函数l:y=-x+6,把y=t(x2-4x+6)+(1-t 2020-07-22 …
已知关于x的一元二次方程x2-2x-t+1=0有两个实数根.(1)求t的取值范围;(2)设v是方程 2020-08-03 …
已知:关于x的一元二次方程tx2-(3t+2)x+2t+2=0(t>0)(1)求证:方程有两个不相 2020-08-03 …