早教吧作业答案频道 -->数学-->
如图,一次函数y=ax+b的图象与反比例函数y=kx的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).(1)利用图中条件,求反比例函数的解析式和m的值;(2)双
题目详情
如图,一次函数y=ax+b的图象与反比例函数y=
的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
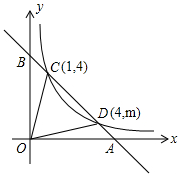
(1)利用图中条件,求反比例函数的解析式和m的值;
(2)双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由.
| k |
| x |

(1)利用图中条件,求反比例函数的解析式和m的值;
(2)双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由.
▼优质解答
答案和解析
(1)把C(1,4)代入y=
,
得k=4,
把(4,m)代入y=
,得m=1;
∴反比例函数的解析式为y=
,m=1;
把C(1,4),D(4,1)代入y=ax+b得出
,
解得
,
∴一次函数的解析式为y=-x+5;
(2)双曲线上存在点P(2,2),使得S△POC=S△POD,理由如下:
∵C点坐标为:(1,4),D点坐标为:(4,1),
∴OD=OC=
,
∴当点P在∠COD的平分线上时,∠COP=∠POD,又OP=OP,
∴△POC≌△POD,
∴S△POC=S△POD.
∵C点坐标为:(1,4),D点坐标为:(4,1),
可得∠COB=∠DOA,
又∵这个点是∠COD的平分线与双曲线的y=
交点,
∴∠BOP=∠POA,
∴P点横纵坐标坐标相等,
即xy=4,x2=4,
∴x=±2,
∵x>0,
∴x=2,y=2,
故P点坐标为(2,2),使得△POC和△POD的面积相等.
利用点CD关于直线y=x对称,P(2,2)或P(-2,-2).
| k |
| x |
得k=4,
把(4,m)代入y=
| 4 |
| x |
∴反比例函数的解析式为y=
| 4 |
| x |
把C(1,4),D(4,1)代入y=ax+b得出
|
解得
|
∴一次函数的解析式为y=-x+5;
(2)双曲线上存在点P(2,2),使得S△POC=S△POD,理由如下:
∵C点坐标为:(1,4),D点坐标为:(4,1),
∴OD=OC=
| 17 |
∴当点P在∠COD的平分线上时,∠COP=∠POD,又OP=OP,
∴△POC≌△POD,
∴S△POC=S△POD.
∵C点坐标为:(1,4),D点坐标为:(4,1),
可得∠COB=∠DOA,
又∵这个点是∠COD的平分线与双曲线的y=
| 4 |
| x |
∴∠BOP=∠POA,
∴P点横纵坐标坐标相等,
即xy=4,x2=4,
∴x=±2,
∵x>0,
∴x=2,y=2,
故P点坐标为(2,2),使得△POC和△POD的面积相等.
利用点CD关于直线y=x对称,P(2,2)或P(-2,-2).
看了 如图,一次函数y=ax+b的...的网友还看了以下:
这几何题怎么算啊?比较简单的,3q!我的想法是:求出斜边和2直角边的长度.1.(求短直角边的长度) 2020-04-26 …
在函数图像中,一个y可不可以有两个对应的x?函数图像中,一个x不可以有两个对应的y,那么y的?是不 2020-05-23 …
我国土地测量中的X坐标和Y坐标都是,分别以南北为X轴还是以东西为X轴.看图的时候怎么看. 2020-06-14 …
在同一平面内,知道a和b的坐标,怎么算c和d的坐标啊?a的坐标是21664000,5072445. 2020-06-14 …
求圆弧坐标在已知圆弧的起点和终点和R,求圆弧的圆心在直角坐标内的坐标!用公式写出了适用任何象限!在 2020-06-14 …
在光滑水平面上,以O点为原点,在该水平面内建立坐标轴Ox,假设空间某一范围内有一沿x轴方向的电场, 2020-06-14 …
知道Y和R,求XR是半径可以用asin和acos一个圆,R是半径,圆上的某一点已知Y坐标,求这点对 2020-06-14 …
一列在竖直方向振动的简谐横波,波长为λ,沿正x方向传播,某一时刻,在振动位移向上且大小等于振幅一半 2020-06-14 …
球的方程:x^2+y^2+z^2=9,求∫(闭合)x^2dx我的疑问:传统的对称法我知道了,我自己 2020-06-14 …
某物体沿x轴运动,它的x坐标与时刻t的函数关系为:x=4t-2t2,则它的初速度和加速度分别是() 2020-06-14 …