如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是()A.作中线AD,再取AD的中点OB.分别作AB、BC的高线,再取此两
如图,三边均不等长的锐角△ABC,若在此三角形内找一点O,使得△OAB、△OBC、△OCA的面积均相等.下列作法中正确的是( )
A. 作中线AD,再取AD的中点O
B. 分别作AB、BC的高线,再取此两高线的交点O
C. 分别作中线AD、BE,再取此两中线的交点O
D. 分别作∠A、∠B的角平分线,再取此两角平分线的交点O
∴O为△ABC的重心,得到AO:OD=2:1,
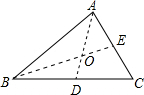
所以△OBC面积为△ABC面积的1:3,
同理△OAB,△OAC的面积也是△ABC面积的1:3.
∴S△OAB=S△BOC=S△OCA,
∴B正确.
故选C.
1.判断a、b、c能否构成三角形的三条边长的条件是().选项:a、a>0&&b>0&&c>0b、a+ 2020-03-31 …
Excel求两条函数公式第一条:A、B、C列偶数与偶数相加、奇数与奇数相加的和,分别在E、F列显示 2020-04-09 …
A、B、C、D四个带电体,已知D带正电,A和C互相排斥,C和B互相吸引,而B和D也互相排斥,则() 2020-06-16 …
用向量证明余弦定理a、b、c都表示向量,|a|、|b|、|c|表示向量的模因为a=b-c所以a^2 2020-07-07 …
在三角形ABC中,内角A、B、C所对边长分别为a、b、c,求证:a^2=b^2+c^2-2向量AB 2020-07-13 …
一个命题的结论是“自然数a,b,c中恰有一个是偶数”,用反证法证明该命题时,正确假设的是()A.a 2020-08-01 …
设a、b、c表示三条直线,α、β表示两个平面,则下列命题中不正确的是()A.c⊥αα∥β⇒c⊥βB. 2020-11-02 …
A、B、C是初中化学常见的物质,A是某种具有吸附性的物质的主要成分,B、C都是氧化物,通常为无色气体 2020-11-05 …
3相电的问题有3条火线分别为A.B.C和一跟零线N用万能表测量有以下情况:A-B\A-C\B-C任意 2020-11-07 …
若实数a,b,c满足loga3<logb3<logc3,则下列关系中不可能成立的()A.a<b<cB 2020-11-12 …