早教吧作业答案频道 -->数学-->
如图,E为正方形ABCD中CD边上一点,∠DAE=30°,P为AE的中点,过点P作直线分别与AD、BC相交于点M、N.若MN=AE,则∠AMN等于.
题目详情
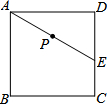
如图,E为正方形ABCD中CD边上一点,∠DAE=30°,P为AE的中点,过点P作直线分别与AD、BC相交于点M、N.若MN=AE,则∠AMN等于___.

▼优质解答
答案和解析
分为两种情况:①如图1,
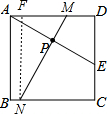
过N作NF⊥AD于F,
则∠NFA=∠MFN=90°,
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠B=∠D=90°,
∴四边形AFNB是矩形,
∴NF=AB=AD,
∵∠NFM=∠D=90°,
在Rt△MFN和Rt△EDA中
∴Rt△MFN≌Rt△EDA(HL),
∴∠AMN=∠AED,
∵∠DAE=30°,∠D=90°,
∴∠AMN=∠AED=180°-30°-90°=60°;
②如图2,
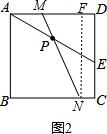
同法可求Rt△MFN≌Rt△EDA,
所以∠FMN=∠AED=60°,
所以∠AMN=180°-60°=120°.
故答案为:60°或120°

过N作NF⊥AD于F,
则∠NFA=∠MFN=90°,
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠B=∠D=90°,
∴四边形AFNB是矩形,
∴NF=AB=AD,
∵∠NFM=∠D=90°,
在Rt△MFN和Rt△EDA中
|
∴Rt△MFN≌Rt△EDA(HL),
∴∠AMN=∠AED,
∵∠DAE=30°,∠D=90°,
∴∠AMN=∠AED=180°-30°-90°=60°;
②如图2,

同法可求Rt△MFN≌Rt△EDA,
所以∠FMN=∠AED=60°,
所以∠AMN=180°-60°=120°.
故答案为:60°或120°
看了如图,E为正方形ABCD中CD...的网友还看了以下:
若非空集合M⊆N={a,b,c,d},则M的个数为8个{a},{b},{c},{d},{a,b}, 2020-05-15 …
4.化简(m-c)/[(m-a)(m-b)]+(b-c)/[(a-b)(m-b)]+(b-c)/[ 2020-05-21 …
在商品价值c+v+m中,用于补偿劳动力价值的是( )A.c B.vC.m D.v+m 2020-06-05 …
在ras算法中,为什么C=m^emodn,D=C^dmodn,D=m其中(e,n)和(d,n)是一 2020-06-20 …
4、下列正确的标识符是:()(A)12ab(B)float(C)b6ty(D)aw~1e(m=a> 2020-06-26 …
1.设abcd是四个整数,且使m=(ab+cd)^2-1/4(a^2+b^2-c^2-d^2)^2 2020-07-09 …
平面α‖平面β,A,C∈α,B,D∈β,M,N分别为AB和CD的中点,求证:MN‖β. 2020-07-30 …
关于连续的一道高等数学题设函数F(X)在闭区间[a,b]上连续,c,d属于(a,b),m,n>0, 2020-08-01 …
以下合法的字符型常量是。A)‘\071’B)"\n"C)‘98’D)"m"以下合法的字符型常量是。A 2020-11-06 …
质点由M点出发做匀加速直线运动,某时刻经过A点,再经过时间n到达B点,再经过时间n到达C点,再经过时 2021-01-13 …