早教吧作业答案频道 -->数学-->
如图所示,6个扇形区域A,B,C,D,E,F,现给这6个区域着色,要求同一个区域涂同一种颜色,相邻的两个区城不得使用同一种颜色,现有4种不同的颜色可用,那么一共有多少种不同的涂色
题目详情
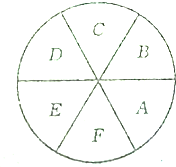
如图所示,6个扇形区域A,B,C,D,E,F,现给这6个区域着色,要求同一个区域涂同一种颜色,相邻的两个区城不得使用同一种颜色,现有4种不同的颜色可用,那么一共有多少种不同的涂色方法?

▼优质解答
答案和解析
(1)当相间区域A、C、E着同一种颜色时,有4种着色方法,此时,B、D、F各有3种着色方法,故有4×3×3×3=108 种方法.
(2)当相间区域A、C、E着色两不同的颜色时,有 4×3×3=36种着色方法,此时B、D、F有 3×2×2=12种着色方法,故共有 432 种着色方法.
(3)当相间区域A、C、E着三种不同的颜色时有 4×3×2=24 种着色方法,此时B、D、F各有2种着色方法.此时共有 24×2×2×2=192种方法.
故总计有108+432+192=732种方法.
(2)当相间区域A、C、E着色两不同的颜色时,有 4×3×3=36种着色方法,此时B、D、F有 3×2×2=12种着色方法,故共有 432 种着色方法.
(3)当相间区域A、C、E着三种不同的颜色时有 4×3×2=24 种着色方法,此时B、D、F各有2种着色方法.此时共有 24×2×2×2=192种方法.
故总计有108+432+192=732种方法.
看了如图所示,6个扇形区域A,B,...的网友还看了以下:
给一个正方体的六个面分别涂上红色或黄色,至少几个面涂了同样的颜色给一个正方体的六个面分别涂上红色或 2020-05-17 …
求解一道数学题(关于计数原理):将一个圆分为3等分,用四种不同颜色给3块区域涂色,要求相邻区域涂不 2020-06-03 …
用五种不同颜色给三棱台ABC-DEF六个顶点涂色,要求每个点涂一种颜色,且每条棱的两个端点涂不同颜 2020-06-12 …
给50个方格分别涂上红色和黄色,使红色和黄色方格数的比是3比2.两种颜色各应涂多少格?列算式 2020-06-18 …
(2014•市中区二模)如图,用四种不同颜色给三棱柱ABC-A1B1C1的六个顶点涂色,要求四种颜 2020-06-20 …
用红、黄、蓝等6种颜色给如图所示的五连圆涂色,要求相邻两个圆所涂颜色不能相同,且红色至少要涂两个圆 2020-07-09 …
高中的数学问题用四种不同颜色给三棱柱的六个顶点涂色,要求每一个点涂一种颜色,且每条棱的两个端点涂不 2020-07-18 …
如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段 2020-07-19 …
请你按要求在圆盘上涂红、黄两种颜色.(1)在如图1的圆盘上涂色,使指针落在红色区域的可能性大.(2 2020-07-21 …
在图形中在给1个格子涂上颜色,使涂色部分成为一个轴对称图形,一共有()种不同的涂法.A.2B.3C 2020-08-03 …