早教吧作业答案频道 -->数学-->
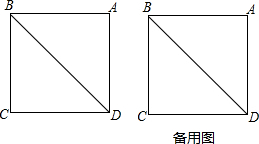
在正方形ABCD中,点H在对角线BD上(与点B、D不重合),连接AH,将HA绕点H顺时针旋转90°与边CD(或CD延长线)交于点P,作HQ⊥BD交射线DC于点Q.(1)如图1:①依题意补全图1;②判断DP与CQ的数
题目详情
在正方形ABCD中,点H在对角线BD上(与点B、D不重合),连接AH,将HA绕点H顺时针旋转90°与边CD(或CD延长线)交于点P,作HQ⊥BD交射线DC于点Q.
(1)如图1:
①依题意补全图1;
②判断DP与CQ的数量关系并加以证明;
(2)若正方形ABCD的边长为
,当 DP=1时,试求∠PHQ的度数.
(1)如图1:
①依题意补全图1;
②判断DP与CQ的数量关系并加以证明;
(2)若正方形ABCD的边长为
| 3 |

▼优质解答
答案和解析
(1)①依题意,补全图形,如图1所示,
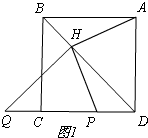
②DP=CQ,
∵HA绕点H顺时针旋转90°,与边CD(或CD延长线)相交于点P,
∴∠AHP=90°,
∴∠AHD+DHP=90°,
∵HQ⊥BD,
∴∠QHD=90°,
∴∠QHP+∠DHP=90°,
∴∠QHP=AHD,
∵四边形ABCD为正方形,
∴∠CDB=∠ADB=45°,AD=CD,
∴∠Q=∠CDB=∠ADB=45°,
∴△QHP≌△DHA,
∴AD=QP,
∴QP=CD,
∴OP-PC=CD-PC,
∴CQ=PD;
(2)①如图2,当点P在边CD上时,连接AP,
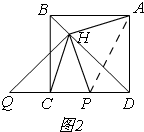
∵正方形的边长为
,PD=1,∠ADP=90°,
∴tan∠APD=
,
∴∠APD=60°,
∵HA=HP,∠AHP=90°,
∴∠APH=45°,
∴∠HPD=∠APH+∠APD=105°,
∵∠Q=45°,
∴∠PHQ=60°,
②如图3,当点P在边CD的延长线时,连接AP,
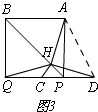
∴∠HPD=∠APD-∠APH=15°,
∵∠HQD=45°,
∴∠PHQ=120°,
∴∠PHQ的度数为120°或60°.

②DP=CQ,
∵HA绕点H顺时针旋转90°,与边CD(或CD延长线)相交于点P,
∴∠AHP=90°,
∴∠AHD+DHP=90°,
∵HQ⊥BD,
∴∠QHD=90°,
∴∠QHP+∠DHP=90°,
∴∠QHP=AHD,
∵四边形ABCD为正方形,
∴∠CDB=∠ADB=45°,AD=CD,
∴∠Q=∠CDB=∠ADB=45°,
∴△QHP≌△DHA,
∴AD=QP,
∴QP=CD,
∴OP-PC=CD-PC,
∴CQ=PD;
(2)①如图2,当点P在边CD上时,连接AP,

∵正方形的边长为
| 3 |
∴tan∠APD=
| 3 |
∴∠APD=60°,
∵HA=HP,∠AHP=90°,
∴∠APH=45°,
∴∠HPD=∠APH+∠APD=105°,
∵∠Q=45°,
∴∠PHQ=60°,
②如图3,当点P在边CD的延长线时,连接AP,

∴∠HPD=∠APD-∠APH=15°,
∵∠HQD=45°,
∴∠PHQ=120°,
∴∠PHQ的度数为120°或60°.
看了在正方形ABCD中,点H在对角...的网友还看了以下:
设有字符序列(Q,H,C,Y,P,A,M,S,R,D,F,X),问新序列(F,H,C,D,P,A,M 2020-05-23 …
( 13 )设有字符序列( Q , H , C , Y , P , A , M , S , R , 2020-05-23 …
设有字符序列(Q,H,C,Y,P,A,M,S,R,D,F,X),则新序列(F,H,C, D,P,A, 2020-05-23 …
设有字符序列(Q,H,C,Y,P,A,M,S,R,D,F,X),问新序列(F,H,C,D,P,A,M 2020-05-23 …
设有字符序列(Q,H,C,Y,P,A,M,S,R,D,F,X),问新序列(F, H,C,D,P,A, 2020-05-24 …
设有字符序列(Q,H,C,Y,P,A,M,S,R,D,F,X),新序列(F, H,C,D,P,A,M 2020-05-24 …
设有字符序列(Q,H,C,Y,P,A, M, S, R, D, F, X),则新序列(F,H,C,D 2020-05-24 …
A.F,H,C,D,P,A,M,Q,R,S,Y,XB.P,A,C,S,Q,D,F,X,R,H,M,Y 2020-05-26 …
已知点B.C.D在同一条直线上,角ABC和角CDE都是等边三角形.BE交AC于点F,AD交CE于点 2020-07-13 …
设一组初始记录关键字序列为(Q,H,C,Y,P,A,M,S,R,D,F,X),则按字母升序的第一趟 2020-07-17 …