求下列双曲线的标准方程:(1)与椭圆=1共焦点且过点(-2)的双曲线.(2)与椭圆=1有共同焦点且在y轴右侧与此椭圆的一个交点的纵坐标为4的双曲线.

题目详情

求下列双曲线的标准方程:

(1)与椭圆 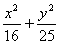=1共焦点且过点(-2 )的双曲线.

(2)与椭圆 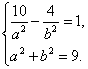=1有共同焦点且在y轴右侧与此椭圆的一个交点的纵坐标为4的双曲线.

▼优质解答

答案和解析

解:(1)由=1知F1(0 -3) F2(0 3).设双曲线的方程为=1(a＞0 b＞0) 则有∴a2=5 b2=4.∴所求的双曲线的方程为=1.(2)由已知得双曲线两焦点分别为F1(0 -3) F2(0 3) 设双曲线的方程为=1(a＞0 b＞0) ∵在y轴右侧双曲线与椭圆有一交点纵坐标为4 ∴它们交点为A( 4).∵||AF1|-|AF2||=2a ∴将A、F1、F2的坐标代入得a=2.又∵c=3 ∴b2=c2-a2=5 故所求双曲线的方程为=1.

看了求下列双曲线的标准方程:(1...的网友还看了以下：

已知椭圆的焦点是F1（0，-1）和F2（0，1），离心率e=12，（I）求此椭圆的标准方程；（Ⅱ）　2020-05-20 …

设一个圆过双曲线x²/9-y²/16=1的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心　2020-06-16 …

椭a2+y2/b2=1(a大于b大于0)的左,右焦点分别为F1F2点P在此椭圆上且PF1垂直PF2 　2020-06-21 …

已知椭圆的焦点是（1）求此椭圆的标准方程（2）设点P在此椭圆上，且有的值　2020-06-21 …

已知三角形三条边的长为3,4,5,圆O的圆心在此三角形的一边上,并且和令两边都相切,则此圆的半径为　2020-07-13 …

已知圆C过双曲线x29-y216=1的一个顶点和一个焦点，且圆心在此双曲线上，则圆心到双曲线中心的　2020-07-26 …

关于椭圆的,解法有疑问已知椭圆X^2/4+Y^2/3=1,试确定M的值.使得在此椭圆上存在不同的两　2020-07-29 …

关于椭圆的数学题已知椭圆方程为：X平方/a平方+Y平方/b平方=1在此椭圆内有一内接正方形,求此正　2020-08-03 …

分别过椭圆x2a2+y2b2=1的左、右焦点F1、F2所作的两条互相垂直的直线l1、l2的交点在此椭　2020-11-01 …

设圆过双曲线x29−y216＝1的一个顶点和一个焦点，圆心在此双曲线上，则圆心到双曲线中心的距离为（　2021-01-23 …