早教吧作业答案频道 -->数学-->
已知△ABC,D、E是射线BC上的两点,且BD=AB,CE=AC.(1)若AB=AC,且∠BAC=90°(如图),求证:AE2=BE•DE;(2)若△ABC是直角三角形,且AE2=BE•DE,求∠ABC的度数.(如果需要,自己画出符合条
题目详情
已知△ABC,D、E是射线BC上的两点,且BD=AB,CE=AC.
(1)若AB=AC,且∠BAC=90°(如图),求证:AE2=BE•DE;
(2)若△ABC是直角三角形,且AE2=BE•DE,求∠ABC的度数.(如果需要,自己画出符合条件的大致图形)
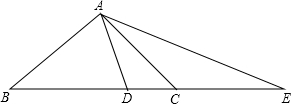
(1)若AB=AC,且∠BAC=90°(如图),求证:AE2=BE•DE;
(2)若△ABC是直角三角形,且AE2=BE•DE,求∠ABC的度数.(如果需要,自己画出符合条件的大致图形)

▼优质解答
答案和解析
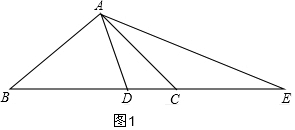 证明:(1)如图1,∵AB=AC,∠BAC=90°,
证明:(1)如图1,∵AB=AC,∠BAC=90°,
∴∠B=∠BCA=45°,
∠BAD=∠BDA=
=67.5°,
∴∠DAC=90°-67.5°=22.5°,
∵AC=CE,
∴∠E=∠CAE=22.5°,
∴∠EAD=45°,
∴∠EAD=∠B,
∵∠E=∠E,
∴△EAD∽△EBA,
∴
=
,
∴AE2=BE•DE;
(2)若△ABC是直角三角形,分三种情况讨论:
①当∠BAC=90°时,如图1,
∵AE2=BE•DE,
∴
=
,
∵∠E=∠E,
∴△ADE∽△BAE,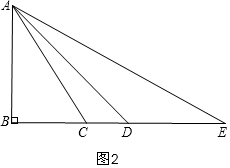
∴∠DAE=∠B,
设∠E=x°,
∵AC=CE,
∴∠CAE=∠E=x°,
∴∠ACB=2x°,
∵∠BAC=90°,
∴∠B=90°-2x°,
∵AB=AD,
∴∠BDA=∠BAD=
=45+x,
在△ADE中,∠DAE=∠B=90-2x,
∠ADB=∠DAE+∠E,
45+x=90-2x+x,
x=22.5°,
∴∠ABC=90-2x=45°;
②当∠ABC=90°时,如图2,
∵AE2=BE•DE,∠E=∠E,
∴△ADE∽△BAE,
但图2中,∠EAD≠∠B,
所以此种情况不成立;
③当∠ACB=90°时,如图3,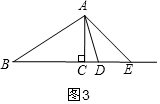
∵AC=CE,
∴∠CAE=∠E=45°,
∵AE2=BE•DE,∠E=∠E,
∴△ADE∽△BAE,
∴∠DAE=∠B,
设∠B=x°,则∠DAE=x°,∠BAC=90°-x°,
∴∠DAC=45°-x°,
∵AB=BD,
∴∠ADB=
=90°-
x°,
由∠BAD=∠ADB得:90-x+45-x=90-
x,
x=30°,
∴∠ABC=30°,
综上所述:∠ABC=45°或30°.
 证明:(1)如图1,∵AB=AC,∠BAC=90°,
证明:(1)如图1,∵AB=AC,∠BAC=90°,∴∠B=∠BCA=45°,
∠BAD=∠BDA=
| 180°-45° |
| 2 |
∴∠DAC=90°-67.5°=22.5°,
∵AC=CE,
∴∠E=∠CAE=22.5°,
∴∠EAD=45°,
∴∠EAD=∠B,
∵∠E=∠E,
∴△EAD∽△EBA,
∴
| AE |
| EB |
| ED |
| AE |
∴AE2=BE•DE;
(2)若△ABC是直角三角形,分三种情况讨论:
①当∠BAC=90°时,如图1,
∵AE2=BE•DE,
∴
| AE |
| BE |
| DE |
| AE |
∵∠E=∠E,
∴△ADE∽△BAE,

∴∠DAE=∠B,
设∠E=x°,
∵AC=CE,
∴∠CAE=∠E=x°,
∴∠ACB=2x°,
∵∠BAC=90°,
∴∠B=90°-2x°,
∵AB=AD,
∴∠BDA=∠BAD=
| 180-(90-2x) |
| 2 |
在△ADE中,∠DAE=∠B=90-2x,
∠ADB=∠DAE+∠E,
45+x=90-2x+x,
x=22.5°,
∴∠ABC=90-2x=45°;
②当∠ABC=90°时,如图2,
∵AE2=BE•DE,∠E=∠E,
∴△ADE∽△BAE,
但图2中,∠EAD≠∠B,
所以此种情况不成立;
③当∠ACB=90°时,如图3,

∵AC=CE,
∴∠CAE=∠E=45°,
∵AE2=BE•DE,∠E=∠E,
∴△ADE∽△BAE,
∴∠DAE=∠B,
设∠B=x°,则∠DAE=x°,∠BAC=90°-x°,
∴∠DAC=45°-x°,
∵AB=BD,
∴∠ADB=
| 180°-x° |
| 2 |
| 1 |
| 2 |
由∠BAD=∠ADB得:90-x+45-x=90-
| 1 |
| 2 |
x=30°,
∴∠ABC=30°,
综上所述:∠ABC=45°或30°.
看了已知△ABC,D、E是射线BC...的网友还看了以下:
有一批果子,平均分给A、B、C三个人后还剩1个;A拿自己得的那份再分成三份给A(自己)、B、C,还剩 2020-03-31 …
5ab的立方×(-四分之三a的立方b的平方)(-三分之二ab的四次方c)的立方 2020-05-13 …
有一批果子,平均分给A、B、C三个人后还剩1个;A拿自己得的那份再分成三份给A(自己)、B、C,还 2020-05-13 …
下图为我国三大自然区局部图,a、b、c是三大自然区的分界线,读图完成下题。1.a、b、c三界线交汇 2020-05-13 …
冬季,来自于A的气流能长驱直人B海湾,其原因是()A.南北跨纬度少B.东西跨经度少C.受地形、地势 2020-05-16 …
三个连续的自然数可以表示为:a-1、a、a+1.这三个连续自然数的和是多少? 2020-05-16 …
逻辑题一道会骑自行车的人比不会骑自行车的人学骑三轮车更困难.由于习惯于骑自行车,会骑自行车的人在骑 2020-05-16 …
三毛的诗如果有来生,要做一颗树,站成永恒,没有悲欢的姿势,一半在土里安详,一半在风中飞扬,一半洒落 2020-05-16 …
请问下面这段话出自三毛的哪部作品?你是我的朋友,但你总要有其他的朋友.你们也许待一起的时间比我长, 2020-05-22 …
三a的平方. 2020-06-03 …