早教吧作业答案频道 -->物理-->
小方和小张设计实验“测量食用油的密度”,请你回答后面的问题:(1)小方的方案:用已经调节平衡的天平测出空烧杯的质量m1,向烧杯内倒入适量食用油,再测出烧杯和食用油的总质量m
题目详情
小方和小张设计实验“测量食用油的密度”,请你回答后面的问题:
(1)小方的方案:用已经调节平衡的天平测出空烧杯的质量m1,向烧杯内倒入适量食用油,再测出烧杯和食用油的总质量m2,然后把烧杯内的食用油全部倒入量筒内,读出量筒内食用油的体积为V1;其测得食用油密度的表达式是:ρ油=___.
(2)小张的方案:在烧杯内倒入适量的食用油,用已经调节平衡的天平测出烧杯和食用油的总质量m3,然后将烧杯内的食用油取适量倒入量筒内,再测出烧杯和剩余食用油的总质量m4,读出量筒内食用油的体积V2,即可测得食用油的密度.
(3)按___的实验方案进行测量,实验误差可以减小一些;如果选择另一种方案,测得油的密度值___(填“偏大”或“偏小”).
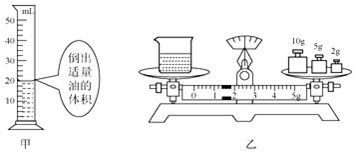
(4)按小张的实验方案进行实验,已测得烧杯和食用油总质量为36.4g.他将烧杯内的食用油取适量倒入量筒后,倒出油的体积如图(甲)所示,烧杯和剩余油的总质量如图(乙)所示,则小张测得食用油的密度为___kg/m3.

(1)小方的方案:用已经调节平衡的天平测出空烧杯的质量m1,向烧杯内倒入适量食用油,再测出烧杯和食用油的总质量m2,然后把烧杯内的食用油全部倒入量筒内,读出量筒内食用油的体积为V1;其测得食用油密度的表达式是:ρ油=___.
(2)小张的方案:在烧杯内倒入适量的食用油,用已经调节平衡的天平测出烧杯和食用油的总质量m3,然后将烧杯内的食用油取适量倒入量筒内,再测出烧杯和剩余食用油的总质量m4,读出量筒内食用油的体积V2,即可测得食用油的密度.
(3)按___的实验方案进行测量,实验误差可以减小一些;如果选择另一种方案,测得油的密度值___(填“偏大”或“偏小”).
(4)按小张的实验方案进行实验,已测得烧杯和食用油总质量为36.4g.他将烧杯内的食用油取适量倒入量筒后,倒出油的体积如图(甲)所示,烧杯和剩余油的总质量如图(乙)所示,则小张测得食用油的密度为___kg/m3.
▼优质解答
答案和解析
(1)所测油的质量为m2-m1,油的密度ρ油=
;
(3)小张的实验方案中所测油的质量与体积时准确的,小张的实验方案误差小;
在小方的实验方案中,油在烧杯壁上有残留,所测油的体积偏小,根据ρ=
,所测油的密度偏大.
(4)由图甲可知,油的体积V=20ml=20cm3,由图乙所示可知,游码标尺的分度值为0.2g,游码对应的刻度1.4g,
烧杯与剩余油的质量为10g+5g+2g+1.4g=18.4g,
倒出油的质量m=36.4g-18.4g=18g,油的密度ρ=
=
=0.9g/cm3=0.9×103kg/m3.
故答案为:(1)
;
(3)小张;偏大;
(4)0.9×103.
| m2-m1 |
| V1 |
(3)小张的实验方案中所测油的质量与体积时准确的,小张的实验方案误差小;
在小方的实验方案中,油在烧杯壁上有残留,所测油的体积偏小,根据ρ=
| m |
| V |
(4)由图甲可知,油的体积V=20ml=20cm3,由图乙所示可知,游码标尺的分度值为0.2g,游码对应的刻度1.4g,
烧杯与剩余油的质量为10g+5g+2g+1.4g=18.4g,
倒出油的质量m=36.4g-18.4g=18g,油的密度ρ=
| m |
| V |
| 18g |
| 20cm3 |
故答案为:(1)
| m2-m1 |
| V1 |
(3)小张;偏大;
(4)0.9×103.
看了 小方和小张设计实验“测量食用...的网友还看了以下:
平行向量是非零向量,那零向量呢?如果A向量和B向量平行,B向量和C向量平行,那A和C向量平不平行呢 2020-04-05 …
已知向量a向量=(3,-2),b向量=(4,1)(1)分别求a向量乘以b向量和a向量加b向量的绝对 2020-05-13 …
在测量密度的实验中:(1)测量食用油密度(实验器材:天平和量筒)方案一:①用调节好的托盘天平测出空 2020-05-13 …
高等数学,向量问题的求助!求高手解答设向量a,b有公共始点,试写出一个与a,b共面且平分a与b的夹 2020-07-11 …
设已知两点MI(2,2,)和M2(1,3,0),计算向量的模、方向余弦和方向角.其中要求方向角αβ 2020-07-25 …
若向量a是任意一非零向量,向量b是模为一的向量,下列各式正确的是1,模a大于模b2,向量a平行于向 2020-07-29 …
空间向量求异面角大小是不是随便选哪个向量都可以?我不知道解题时该选区哪个向量来求,貌似去相反向量答 2020-07-31 …
给出下列命题:⑴若向量a^2+b^2=0,则向量a=b=0;⑵若a、b、c是三个非零向量,向量a+b 2020-12-07 …
已知向量e1,e2,e3为不共线的非零向量,向量a=-e1+3e2+2e3,向量b=4e1-6e2+ 2020-12-07 …
下列结论中正确的是:A零向量与零向量的和是实数0B对任一向量a,有a向量-a向量=零向量C对任意两个 2020-12-23 …