早教吧作业答案频道 -->数学-->
我边防局接到情报,在海礁AB所在直线l的一侧点M处有走私团伙在进行交易活动,边防局迅速派出快艇前去搜捕.如图,已知快艇出发位置在l的另一侧码头P处,PA=8公里,PB=10公里,∠APB=60°
题目详情
我边防局接到情报,在海礁AB所在直线l的一侧点M处有走私团伙在进行交易活动,边防局迅速派出快艇前去搜捕.如图,已知快艇出发位置在l的另一侧码头P处,PA=8公里,PB=10公里,∠APB=60°.
(1)是否存在点M,使快艇沿航线P→A→M或P→B→M的路程相等.如存在,则建立适当的直角坐标系,求出点M的轨迹方程,且画出轨迹的大致图形;如不存在,请说明理由.
(2)问走私船在怎样的区域上时,路线P→A→M比路线P→B→M的路程短,请说明理由.

(1)是否存在点M,使快艇沿航线P→A→M或P→B→M的路程相等.如存在,则建立适当的直角坐标系,求出点M的轨迹方程,且画出轨迹的大致图形;如不存在,请说明理由.
(2)问走私船在怎样的区域上时,路线P→A→M比路线P→B→M的路程短,请说明理由.
▼优质解答
答案和解析
(1)建立如图所示的坐标系,|MA|-|MB|=2,
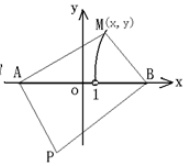
∴M的轨迹是双曲线的右支,|AB|=
=2
,
∴a=1,c=
,b2=20,
∴M的轨迹方程是x2-
=1(x>1,y>0);
(2)走私船在直线l的左侧,且在(1)中曲线的左侧的区域时,路线P→A→M最短.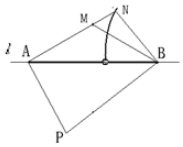
理由:设AM的延长线与(1)中曲线交于点N,则PA+AN=PB+BN,
PA+AM=PA+AN-MN=PB+BN-MN<PB+BM.

∴M的轨迹是双曲线的右支,|AB|=
| 64+100-80 |
| 21 |
∴a=1,c=
| 21 |
∴M的轨迹方程是x2-
| y2 |
| 20 |
(2)走私船在直线l的左侧,且在(1)中曲线的左侧的区域时,路线P→A→M最短.

理由:设AM的延长线与(1)中曲线交于点N,则PA+AN=PB+BN,
PA+AM=PA+AN-MN=PB+BN-MN<PB+BM.
看了我边防局接到情报,在海礁AB所...的网友还看了以下:
己知PE、PF是O的切线,A、B是一组对径点,PB交O于另一点C,直线AF、BE交于D点.求证:∠ 2020-04-07 …
1.A,B是平面上俩点,AB=10cm,P为平面上一点,若PA+PB=20cm,则P点——2.以平 2020-05-13 …
练习:1.右图一中,P为直线m外一点,A,B,C为m上不同的三点且PB⊥m,那麼()(A)PA,P 2020-06-17 …
(2014•赤峰样卷)如图,过点A(0,3)的直线l1与x轴交于点B,tan∠ABO=34.过点A 2020-06-19 …
提出问题:如图1,将三角板放在正方形ABCD上,使三角板的直角顶点P在对角线AC上,一条直角边经过 2020-06-20 …
P是圆外一点,PA,PB分别和⊙O相切于A,B,PA=PB=4CMP是圆外一点,PA,PB分别和圆 2020-07-20 …
如图,P为x轴上任意一点,PB垂直于x轴,交直线y=0.5x、y=kx于A、B两点,BC⊥PB交直 2020-07-29 …
如图,AB是圆O的直径,P为圆外一点,PB是圆O的切线,PA是圆O的割线且与圆O相交于点C.过点C 2020-07-31 …
已知:A.B是圆x2+y2=4与x轴的两个交点,P为直线l:x=4上的动点,PA.PB与圆x^2+ 2020-07-31 …
已知:点A、B都在半径为9的圆O上,P是射线OA上一点,以PB为半径的圆P与圆O相交的另一个交点为 2020-08-01 …