早教吧作业答案频道 -->数学-->
有一款灯,内有两面镜子AB、BC,当光线经过镜子反射时,入射角等于反射角,即图1、图2中的∠1=∠2,∠3=∠4.(1)如图1,当AB⊥BC时,说明为什么进入灯内的光线EF与离开灯的光线GH互相平
题目详情
有一款灯,内有两面镜子AB、BC,当光线经过镜子反射时,入射角等于反射角,即图1、图2中的∠1=∠2,∠3=∠4.
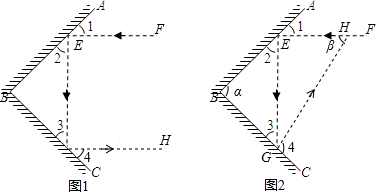
(1)如图1,当AB⊥BC时,说明为什么进入灯内的光线EF与离开灯的光线GH互相平行.
(2)如图2,若两面镜子的夹角为α°(0<α<90)时,进入灯内的光线与离开灯的光线的夹角为β°(0<β<90),试探索α与β的数量关系.
(3)若两面镜子的夹角为α°(90<α<180),进入灯内的光线与离开灯的光线所在直线的夹角为β°(0<β<90).直接写出α与β的数量关系.

(1)如图1,当AB⊥BC时,说明为什么进入灯内的光线EF与离开灯的光线GH互相平行.
(2)如图2,若两面镜子的夹角为α°(0<α<90)时,进入灯内的光线与离开灯的光线的夹角为β°(0<β<90),试探索α与β的数量关系.
(3)若两面镜子的夹角为α°(90<α<180),进入灯内的光线与离开灯的光线所在直线的夹角为β°(0<β<90).直接写出α与β的数量关系.
▼优质解答
答案和解析
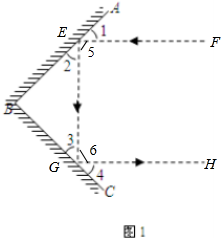 (1)证明:如图1所示:
(1)证明:如图1所示:
∵∠1=∠2,
又∵∠5=180°-∠1-∠2=180°-2∠,
∴∠5=180°-2∠2,
同理∠6=180°-2∠3,
∵∠+∠3=90°,
∴∠5+∠6=180°,
∴EF∥GH,
即进入灯内的光线EF与离开灯的光线GH互相平行.
(2) 2α+β=180°,理由如下:
如图2所示: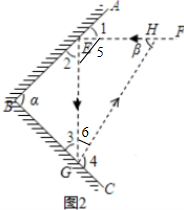
由(1)所证,有∠5=180°-2∠2,∠6=180°-2∠3,
∵∠2+∠3=180°-∠α,
∴∠β=180°-∠5-∠6=2(∠2+∠3)-180°=2(180°-∠α)-180°=180°-2∠α,
∴α与β的数量关系为:2α+β=180°,
(3) 2α-β=180°.
 (1)证明:如图1所示:
(1)证明:如图1所示:∵∠1=∠2,
又∵∠5=180°-∠1-∠2=180°-2∠,
∴∠5=180°-2∠2,
同理∠6=180°-2∠3,
∵∠+∠3=90°,
∴∠5+∠6=180°,
∴EF∥GH,
即进入灯内的光线EF与离开灯的光线GH互相平行.
(2) 2α+β=180°,理由如下:
如图2所示:
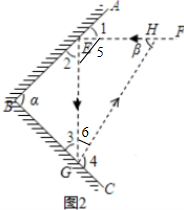
由(1)所证,有∠5=180°-2∠2,∠6=180°-2∠3,
∵∠2+∠3=180°-∠α,
∴∠β=180°-∠5-∠6=2(∠2+∠3)-180°=2(180°-∠α)-180°=180°-2∠α,
∴α与β的数量关系为:2α+β=180°,
(3) 2α-β=180°.
看了有一款灯,内有两面镜子AB、B...的网友还看了以下:
有关如图所示各图象的说法中,不正确的是()A.图甲为小灯泡灯丝中的电流与灯泡两端电压的关系图象B. 2020-05-02 …
图甲中的A、B分别为小灯泡和定值电阻的I-U图象,小灯泡和电阻的连接情况如图乙所示,电源电压8V, 2020-05-02 …
阅读短文,回答问题.现在很多马路上都应用LED灯作路灯,这种LED灯是通过光电转换来供电的.右图是 2020-05-13 …
一个标有“12V”,功率未知的灯泡,测得灯丝电阻R随灯泡两端电压变化的关系图线如图所示,利用这条图 2020-05-14 …
图一图二①图一是哪一位科学家?②图二是他的发明灯泡,它的灯丝是什么?③这位科学家被称为什么? 2020-05-15 …
如图所示的是两只普通照明灯泡的I-U图象(1)据图象求出两只灯泡的额定功率和正常发光时的电阻;(2 2020-05-15 …
一小灯泡的伏安特性曲线如图所示,图中只画出了AB段,由图可知,当灯泡两端电压由3V变为6V时,则灯 2020-05-17 …
荧光灯和栅格灯的区别,图书馆选用什么样的比较好?为什么大多的图上之花荧光灯呢 2020-05-17 …
如图所示电路中,三个相同的灯泡额定功率是40w,在不损坏灯泡的情况下,这三个灯泡消耗的总功率最大不 2020-06-05 …
这张开关电灯(图)N,L,FU,IN,SA1,SA2,123,各代表是什么?IN是灯泡.SA1/2 2020-06-14 …