早教吧作业答案频道 -->数学-->
如图,已知抛物线经过点A(-1,0),B(3,0),C(0,3)三点.(1)求抛物线的解析式;(2)点M是线段BC上的点(不与B、C重合),过M作NM∥y轴交抛物线于N,若点M的横坐标为m,请用含m
题目详情
如图,已知抛物线经过点A(-1,0),B(3,0),C(0,3)三点.
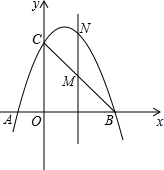
(1)求抛物线的解析式;
(2)点M是线段BC上的点(不与B、C重合),过M作NM∥y轴交抛物线于N,若点M的横坐标为m,请用含m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点m,使△BNC的面积最大?若存在,求m的值和△BNC的面积;若不存在,说明理由.
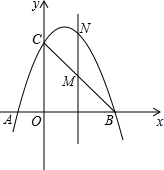
(1)求抛物线的解析式;
(2)点M是线段BC上的点(不与B、C重合),过M作NM∥y轴交抛物线于N,若点M的横坐标为m,请用含m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点m,使△BNC的面积最大?若存在,求m的值和△BNC的面积;若不存在,说明理由.
▼优质解答
答案和解析
(1)∵抛物线经过点A(-1,0),B(3,0),C(0,3)三点,
∴设抛物线的解析式为:y=a(x+1)(x-3),
把C(0,3)代入得:3=a(0+1)(0-3),
a=-1,
∴y抛物线的解析式:y=-x2+2x+3;
(2)设直线BC的解析式为:y=kx+b,
把B(3,0),C(0,3)代入得:
,
解得:
,
∴直线BC的解析式为y=-x+3,
∴M(m,-m+3),
又∵MN⊥x轴,
∴N(m,-m2+2m+3),
∴MN=(-m2+2m+3)-(-m+3)=-m2+3m(0<m<3);
(3)存在,
S△BNC=S△CMN+S△MNB=
|MN|•|OB|,
∴当|MN|最大时,△BNC的面积最大,
MN=-m2+3m=-(m-
)2+
,
当m=
时,MN的有最大值为
,
所以当m=
时,△BNC的面积最大为
×
×3=
.
∴设抛物线的解析式为:y=a(x+1)(x-3),
把C(0,3)代入得:3=a(0+1)(0-3),
a=-1,
∴y抛物线的解析式:y=-x2+2x+3;
(2)设直线BC的解析式为:y=kx+b,
把B(3,0),C(0,3)代入得:
|
解得:
|
∴直线BC的解析式为y=-x+3,
∴M(m,-m+3),
又∵MN⊥x轴,
∴N(m,-m2+2m+3),
∴MN=(-m2+2m+3)-(-m+3)=-m2+3m(0<m<3);
(3)存在,
S△BNC=S△CMN+S△MNB=
| 1 |
| 2 |
∴当|MN|最大时,△BNC的面积最大,
MN=-m2+3m=-(m-
| 3 |
| 2 |
| 9 |
| 4 |
当m=
| 3 |
| 2 |
| 9 |
| 4 |
所以当m=
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
| 27 |
| 8 |
看了如图,已知抛物线经过点A(-1...的网友还看了以下:
韦达定理 已知一元二次方程8X-(m-1)X+M-7=0 M为何实数时,方程的两个根互为相反数一. 2020-05-16 …
屏幕上用“*”显示0-360度的余弦函数cos(x)曲线#include #include int 2020-05-16 …
如果用M表示集合(0,1),那么下面写法正确的是A.0∈M B.1∈M C.(0,1)∈M D.{ 2020-05-17 …
已知2mx-y-8m+3=0,圆c:x^2+y^2-6x-12y+20=0,(1)M∈R,证明:l 2020-05-21 …
帮忙求个递推公式,从兔子繁殖问题衍生而来.m(0)=1,m(1)=1,m(2)=1,m(3)=2, 2020-08-01 …
关于韦达定理的问题1.已知一元二次方程(m-1)x^2+(3m^2-27)x+(m-4)=0,(1 2020-08-02 …
已知关于x的方程(m^2-1)x^2-(m+1)x+m=0(1)m为何值时,此方程是一元—次已知关于 2020-11-12 …
向量的集合部分问题设M=﹛a|a=(2,0)+m(0,1),m∈R﹜和N=﹛b|b=(1,1)+n( 2020-11-30 …
有带电平行板电容器竖直安放如图所示,两板间距d="0.1"m,电势差U="1000"V,现从平行板上 2020-12-06 …
分类讨论已知函数f(x)=1-1/x(x>=1)1/x-1(00,∴0∈[a,b],矛盾我的理解:① 2020-12-24 …