早教吧作业答案频道 -->数学-->
已知二次函数y=-x2+(m-1)x+m.(1)证明:不论m取何值,该函数图象与x轴总有公共点;(2)若该函数的图象与y轴交点于(0,3),求出顶点坐标并画出该函数;(3)在(2)的条件下,观察
题目详情
已知二次函数y=-x2+(m-1)x+m.
(1)证明:不论m取何值,该函数图象与x轴总有公共点;
(2)若该函数的图象与y轴交点于(0,3),求出顶点坐标并画出该函数;
(3)在(2)的条件下,观察图象,不等式-x2+(m-1)x+m>3的解集是___.

(1)证明:不论m取何值,该函数图象与x轴总有公共点;
(2)若该函数的图象与y轴交点于(0,3),求出顶点坐标并画出该函数;
(3)在(2)的条件下,观察图象,不等式-x2+(m-1)x+m>3的解集是___.
▼优质解答
答案和解析
(1)证明:令y=0,得到-x2+(m-1)x+m=0,
∵a=-1,b=m-1,c=m,
∴b2-4ac=(m-1)2+4m=(m+1)2,
又(m+1)2≥0,即b2-4ac≥0,
∴方程y=-x2+(m-1)x+m有实数根,
则该函数图象与x轴总有公共点;
(2) ∵该函数的图象与y轴交于点(0,3),
∴把x=0,y=3代入解析式得:m=3,
∴y=-x2+2x+3=-(x-1)2+4,
∴顶点坐标为(1,4);
列表如下:
描点;
画图如下:
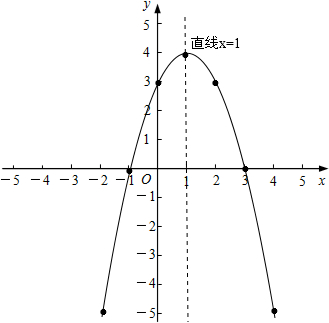
(3) 由图象可得:不等式-x2+(m-1)x+m>3的解集是0故答案为0
∵a=-1,b=m-1,c=m,
∴b2-4ac=(m-1)2+4m=(m+1)2,
又(m+1)2≥0,即b2-4ac≥0,
∴方程y=-x2+(m-1)x+m有实数根,
则该函数图象与x轴总有公共点;
(2) ∵该函数的图象与y轴交于点(0,3),
∴把x=0,y=3代入解析式得:m=3,
∴y=-x2+2x+3=-(x-1)2+4,
∴顶点坐标为(1,4);
列表如下:
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | -5 | 0 | 3 | 4 | 3 | 0 | -5 |
画图如下:

(3) 由图象可得:不等式-x2+(m-1)x+m>3的解集是0
看了已知二次函数y=-x2+(m-...的网友还看了以下:
对于虚析构函数与一般虚函数,以下说法正确的是A、重定义函数就是派生类的构造函数B、重定义函数就是派 2020-04-06 …
两道关于求证周期函数的问题1.已知f(x)是奇函数,且f(x)的图像关于直线x=2对称,求证:f( 2020-06-02 …
复合函数的定义域求外函数的定义域已知复合函数f(根号下x)=(1/x)+2(根号下x),求f(x) 2020-06-05 …
已知函数y=fx,x属于R,对于任意的x,y属于R,fx+y=fx+fy,求证:f0=0,且fx是 2020-06-09 …
已知fx的定义域为x不等于0的全体实数且对于任意x1,x2,都有f(x1x2)=f(x1)+f(x 2020-07-13 …
已知函数f(x)=2x平方-1.用定义证明f(x)在(-无穷,0]上是减函数;求函数f(x)在x属 2020-07-25 …
已知关于x的函数y=ax2+x+1(a为常数)(1)若函数的图象与坐标轴恰有两个交点,求a的值;( 2020-07-26 …
反比例函数曲线中点坐标怎么求.例如点A(1,4)点B(2,2)在反比例函数y=...反比例函数曲线 2020-07-29 …
请问这道题怎样做?已知函数f(x)=lg(2+x)-lg(a-x)是奇函数!1:求实数a的值;2: 2020-08-01 …
函数在某个区间上单调递增(递减)的为什么要其导函数大于等于零(小于等于零)恒成立.而如果有一个函数 2020-08-02 …