早教吧作业答案频道 -->数学-->
如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1,(1)当∠A为70°时,则∠A1的度数是°;当∠A=90°时,∠A1的度数是°;(2)①探索∠A与∠A1之间数量关系并
题目详情
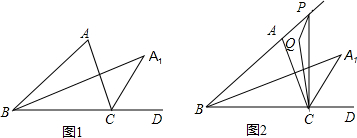
如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1,
(1)当∠A为70°时,则∠A1的度数是___°;当∠A=90°时,∠A1的度数是___°;
(2)①探索∠A与∠A1之间数量关系并证明你的结论;
②若∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、An,请你直接写出∠An与∠A的数量关系___;
(3)如图,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,随着点P的运动,∠Q+∠A1的值是否变化?若变化,请说名理由;若不变,请求出其值.
(1)当∠A为70°时,则∠A1的度数是___°;当∠A=90°时,∠A1的度数是___°;
(2)①探索∠A与∠A1之间数量关系并证明你的结论;
②若∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、An,请你直接写出∠An与∠A的数量关系___;
(3)如图,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,随着点P的运动,∠Q+∠A1的值是否变化?若变化,请说名理由;若不变,请求出其值.

▼优质解答
答案和解析
(1)∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=
∠ABC,∠A1CD=
∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴
(∠A+∠ABC)=
∠ABC+∠A1,
∴∠A1=
∠A,
∵∠A=70°,
∴∠A1=35°
∵∠A=90°,
∴∠A1=45°;
故答案为:35,45;
(2)①∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=
∠ABC,∠A1CD=
∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴
(∠A+∠ABC)=
∠ABC+∠A1,
∴∠A1=
∠A;
②同②可求得:
∠A2=
∠A1=
∠A,
∠A3=
∠A2=
∠A,
…
依此类推,∠An=
∠A;
故答案为:∠An=
∠A;
(3)△ABC中,由三角形的外角性质知:∠BAC=∠AEC+∠ACE=2(∠QEC+∠QCE);
即:2∠A1=2(180°-∠Q),
化简得:∠A1+∠Q=180°.
∴∠A1BC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴∠A1=
| 1 |
| 2 |
∵∠A=70°,
∴∠A1=35°
∵∠A=90°,
∴∠A1=45°;
故答案为:35,45;
(2)①∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴∠A1=
| 1 |
| 2 |
②同②可求得:
∠A2=
| 1 |
| 2 |
| 1 |
| 22 |
∠A3=
| 1 |
| 2 |
| 1 |
| 23 |
…
依此类推,∠An=
| 1 |
| 2n |
故答案为:∠An=
| 1 |
| 2n |
(3)△ABC中,由三角形的外角性质知:∠BAC=∠AEC+∠ACE=2(∠QEC+∠QCE);
即:2∠A1=2(180°-∠Q),
化简得:∠A1+∠Q=180°.
看了如图,△ABC中,∠ABC的角...的网友还看了以下:
a是b的倍数,c是a的倍数(a、c不相同),下列判断错误的是()A、a与b的和也一定是b的倍数B、a 2020-03-30 …
设a=(√5-1)/2,求(a^5+a^4-2a^3-a^2-a+2)/a^3-a∵2a=√5-1 2020-04-05 …
线性代数证明,设A是n阶方阵,且A的平方等于En,证明R(A+E)+R(A-E)设A是n阶方阵,且 2020-04-05 …
三阶实对称矩阵,R(A)=2,A^2+2A=0,求特征值.都得到a(a+2)=0.为什么得到a=0 2020-04-13 …
设A为n阶可逆矩阵,A*是A的伴随矩阵,则|A*|=()A.|A|B.1|A|C.|A|*D.|A 2020-05-14 …
设A为n阶非零方阵,A*是A的伴随矩阵,A′是A的转置矩阵,当A*=A′时,证明|A|≠0. 2020-05-14 …
线性代数证明题27.设A是m×n实矩阵,n<m,且线性方程组Ax=b有惟一解.证明ATA是可逆矩阵 2020-05-14 …
线性代数题:设A为n阶方阵,A*是A的伴随矩阵,如果/A/=a≠0,则/A*/=()设A为n阶方阵 2020-05-15 …
a是不为1的有理数,我们把(1-a)分之1称为a的差倒数.如:2的差倒数是(1-2)分之1=-1, 2020-05-16 …
超难数学题,1.一件商品的成本是a元,在售价中以b元售出(b大于a),这件商品的销售盈利率为——% 2020-05-21 …