早教吧作业答案频道 -->数学-->
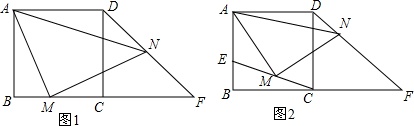
如图,正方形ABCD,AM⊥MN,DN交BC延长线于F.(1)如图1,M为BC中点,AM=MN,则△CDF的形状是;(2)如图2,E是AB上一动点,M为EC中点,CF=CD,则AM与MN有怎样的数量关系?并证明你的结论.
题目详情
如图,正方形ABCD,AM⊥MN,DN交BC延长线于F.
(1)如图1,M为BC中点,AM=MN,则△CDF的形状是___;
(2)如图2,E是AB上一动点,M为EC中点,CF=CD,则AM与MN有怎样的数量关系?并证明你的结论.
(1)如图1,M为BC中点,AM=MN,则△CDF的形状是___;
(2)如图2,E是AB上一动点,M为EC中点,CF=CD,则AM与MN有怎样的数量关系?并证明你的结论.

▼优质解答
答案和解析
(1)△CDF是等腰直角三角形;理由如下:
作NG⊥CF于G,如图1所示: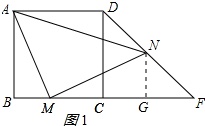
则∠MGN=90°,NG∥CD,
∵四边形ABCD是正方形,
∴AB=BC=CD,∠B=∠BCD=90°,
∴∠DCF=90°,∠BAM+∠AMB=90°,
∵AM⊥MN,
∴∠AMN=90°,
∴∠AMB+∠NMG=90°,
∴∠BAM=∠GMN,
在△ABM和△MGN中,
,
∴△ABM≌△MGN(AAS),
∴BM=GN,AB=MG,
∵M是BC的中点,
∴BM=CM=
BC,
∴GN=
BC=
CD,CG=CM,
∴GN是△CDF的中位线,
∴G是CF的中点,
∴CD=CF,
∴△CDF是等腰直角三角形;
故答案为:等腰直角三角形.
(2)AM=MN;理由如下:
连接BM、DM;如图2所示: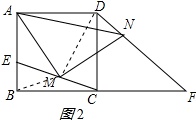
∵M为EC中点,∠B=90°,
∴MB=
EC=MC=EM,
∴∠MBC=∠MCB,
∴∠ABM=∠DCM,
在△ABM和△DCM中,
,
∴△ABM≌△DCM(SAS),
∴AM=DM,
∴∠MAD=∠ADM,
设∠MAD=∠ADM=x,
∴∠MDC=90°-x,
∴∠DMN=90°-(180°-2x)=2x-90°,
∵CF=CD,
∴∠F=∠CDF=45°,
∴∠MDN=135°-x,
∴∠DNM=180°-∠MDN-∠DMN=180°-(90°-x+45°)-(2x-90°)=135°-x,
∴∠MDN=∠MND,
∴MN=MD,
∴AM=MN.
作NG⊥CF于G,如图1所示:

则∠MGN=90°,NG∥CD,
∵四边形ABCD是正方形,
∴AB=BC=CD,∠B=∠BCD=90°,
∴∠DCF=90°,∠BAM+∠AMB=90°,
∵AM⊥MN,
∴∠AMN=90°,
∴∠AMB+∠NMG=90°,
∴∠BAM=∠GMN,
在△ABM和△MGN中,
|
∴△ABM≌△MGN(AAS),
∴BM=GN,AB=MG,
∵M是BC的中点,
∴BM=CM=
| 1 |
| 2 |
∴GN=
| 1 |
| 2 |
| 1 |
| 2 |
∴GN是△CDF的中位线,
∴G是CF的中点,
∴CD=CF,
∴△CDF是等腰直角三角形;
故答案为:等腰直角三角形.
(2)AM=MN;理由如下:
连接BM、DM;如图2所示:

∵M为EC中点,∠B=90°,
∴MB=
| 1 |
| 2 |
∴∠MBC=∠MCB,
∴∠ABM=∠DCM,
在△ABM和△DCM中,
|
∴△ABM≌△DCM(SAS),
∴AM=DM,
∴∠MAD=∠ADM,
设∠MAD=∠ADM=x,
∴∠MDC=90°-x,
∴∠DMN=90°-(180°-2x)=2x-90°,
∵CF=CD,
∴∠F=∠CDF=45°,
∴∠MDN=135°-x,
∴∠DNM=180°-∠MDN-∠DMN=180°-(90°-x+45°)-(2x-90°)=135°-x,
∴∠MDN=∠MND,
∴MN=MD,
∴AM=MN.
看了如图,正方形ABCD,AM⊥M...的网友还看了以下:
在三角形ABC中,角A,B,C所对的边分别为a,b,c,若a+b=c(cosA+cosB)(1)判 2020-04-07 …
1.已知三角形ABC(a+b+c)(b+c+a)=3bcSinA=2sinBcosC判断三角形AB 2020-05-14 …
已知A(1/3,1/a),B(1/4,1/b),C(1/5,1/c)满足a/(b+c)=1/3,b 2020-05-16 …
三角形的顶点坐标分别是A(2,2),B(3,0)三角形的顶点坐标分别是A(2,2),B(3,0), 2020-05-16 …
将10/1化成a/1+b/1+c/1形式.其中a,b,c为自然数,且它们最大公约数为1,a,b,c 2020-05-21 …
COSA+2COSBCOSC=1,判断三角形的形状因为A+B+C=180所以cos(180-(B+ 2020-07-16 …
已知扇形的圆心角是α,所在圆的半径是R,若扇形的周长是一定值C(C>0)当α为多少弧度时,该扇形的 2020-07-26 …
1.已知a,b,c满足ab+a+b=bc+b+c=ca+c+a=3求(a+1)(b+1(c+1)的 2020-08-01 …
若a、b、c为三角形的三边长,且方程a(1+x)2+2bx-c(1-x2)=0的两根相等,则此三角形 2020-11-07 …
看看是什么三角形以知三角形ABC的三边分别为abc,且满足1/a-1/b+1/c=1/a-b+c试判 2020-12-25 …