早教吧作业答案频道 -->数学-->
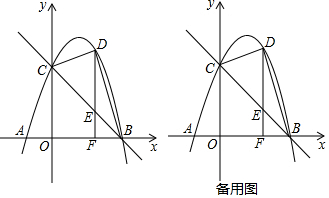
如图,已知抛物线y=a(x+1)(x-5)与x轴从左至右交于A,B两点,与y轴交于点C(0,5).(1)求该抛物线的函数解析式;(2)D是第一象限内抛物线上的一个动点(与点C,B不重合),过点D作
题目详情
如图,已知抛物线y=a(x+1)(x-5)与x轴从左至右交于A,B两点,与y轴交于点C(0,5).
(1)求该抛物线的函数解析式;
(2)D是第一象限内抛物线上的一个动点(与点C,B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,CD,直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.
(3)若M为抛物线对称轴上一动点,△MBC为直角三角形,请直接写出点M的坐标.
(1)求该抛物线的函数解析式;
(2)D是第一象限内抛物线上的一个动点(与点C,B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,CD,直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.
(3)若M为抛物线对称轴上一动点,△MBC为直角三角形,请直接写出点M的坐标.

▼优质解答
答案和解析
(1)把C(0,5)代入y=a(x+1)(x-5)得-5a=5,解得a=-1,
所以抛物线解析式为y=-(x+1)(x-5),即y=-x2+4x+5;
(2)能.
当y=0时,-(x+1)(x-5)=0,解得x1=-1,x2=5,则A(-1,0),B(5,0),
设直线BC的解析式为y=kx+b,
把C(0,5),B(5,0)代入得
,解得
,
所以直线BC的解析式为y=-x+5,
设D(x,-x2+4x+5),则E(x,-x+5),F(x,0),(0<x<5),
∴DE=-x2+4x+5-(-x+5)=-x2+5x,EF=-x+5,
当DE:EF=2:3时,S△BDE:S△BEF=2:3,即(-x2+5x):(-x+5)=2:3,
整理得3x2-17x+10=0,解得x1=
,x2=5(舍去),此时D点坐标为(
,
);
当DE:EF=3:2时,S△BDE:S△BEF=3:2,即(-x2+5x):(-x+5)=3:2,
整理得2x2-13x+15=0,解得x1=
,x2=5(舍去),此时D点坐标为(
,
);
综上所述,当点D的坐标为(
,
)或(
,
)时,直线BC能否把△BDF分成面积之比为2:3的两部分;
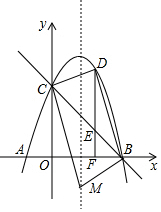
(3)抛物线的对称轴为直线x=2,如图,
设M(2,t),
∵B(5,0),C(0,5),
∴BC2=52+52=50,MC2=22+(t-5)2=t2-10t+29,MB2=(2-5)2+t2=t2+9,
当BC2+MC2=MB2时,△BCM为直角三角形,∠BCM=90°,即50+t2-10t+29=t2+9,解得t=7,此时M点的坐标为(2,7);
当BC2+MB2=MC2时,△BCM为直角三角形,∠CBM=90°,即50+t2+9=t2-10t+29,解得t=-3,此时M点的坐标为(2,-3);
当MC2+MM2=BC2时,△BCM为直角三角形,∠CMB=90°,即t2-10t+29+t2+9=50,解得t1=6,t2=-1,此时M点的坐标为(2,6)或(2,-1),
综上所述,满足条件的M点的坐标为(2,7),(2,-3),(2,6),(2,-1).
所以抛物线解析式为y=-(x+1)(x-5),即y=-x2+4x+5;
(2)能.
当y=0时,-(x+1)(x-5)=0,解得x1=-1,x2=5,则A(-1,0),B(5,0),
设直线BC的解析式为y=kx+b,
把C(0,5),B(5,0)代入得
|
|

所以直线BC的解析式为y=-x+5,
设D(x,-x2+4x+5),则E(x,-x+5),F(x,0),(0<x<5),
∴DE=-x2+4x+5-(-x+5)=-x2+5x,EF=-x+5,
当DE:EF=2:3时,S△BDE:S△BEF=2:3,即(-x2+5x):(-x+5)=2:3,
整理得3x2-17x+10=0,解得x1=
| 2 |
| 3 |
| 2 |
| 3 |
| 65 |
| 9 |
当DE:EF=3:2时,S△BDE:S△BEF=3:2,即(-x2+5x):(-x+5)=3:2,
整理得2x2-13x+15=0,解得x1=
| 3 |
| 2 |
| 3 |
| 2 |
| 35 |
| 4 |
综上所述,当点D的坐标为(
| 2 |
| 3 |
| 65 |
| 9 |
| 3 |
| 2 |
| 35 |
| 4 |
(3)抛物线的对称轴为直线x=2,如图,
设M(2,t),
∵B(5,0),C(0,5),
∴BC2=52+52=50,MC2=22+(t-5)2=t2-10t+29,MB2=(2-5)2+t2=t2+9,
当BC2+MC2=MB2时,△BCM为直角三角形,∠BCM=90°,即50+t2-10t+29=t2+9,解得t=7,此时M点的坐标为(2,7);
当BC2+MB2=MC2时,△BCM为直角三角形,∠CBM=90°,即50+t2+9=t2-10t+29,解得t=-3,此时M点的坐标为(2,-3);
当MC2+MM2=BC2时,△BCM为直角三角形,∠CMB=90°,即t2-10t+29+t2+9=50,解得t1=6,t2=-1,此时M点的坐标为(2,6)或(2,-1),
综上所述,满足条件的M点的坐标为(2,7),(2,-3),(2,6),(2,-1).
看了 如图,已知抛物线y=a(x+...的网友还看了以下:
交流和直流转换中能量的变化假如把一个220V交流变成高压交流,那能量怎么变化啊,我记得要遵循能量守恒 2020-03-30 …
为什么ax+by+c+A(mx+ny+p)表示过直线ax+by+c=0与mx+ny+p=0交点的所 2020-04-27 …
人能和什么物种进行交流?如题,今天有人突然说我不是人,是狗.嗯,这个问题很深奥,人都能和那些物种交 2020-05-13 …
关于速度的猜想见下.请问物理高手们有什么看法?一个再简单不过的现象.将两条直线相交就有一个交点,如 2020-05-14 …
英语翻译首先,为什么不参加一个英语俱乐部,(First,waynot……)如果你这么做,你会交到很 2020-05-14 …
1.比如一个三次函数其本身图像又两个极值点(对应有极值)与x轴有三个交点,但是导函数图像(二次函数 2020-05-17 …
无友不如己者,这句话你们是怎样理解的?那天老板开会,无意间提到交朋友,他说交朋友一定要交比自己能力 2020-05-20 …
一次函数y=-x和反比例函数y=k/x可能无交点吗?可能只有一个交点吗,可能有两个交点吗,若可能, 2020-05-21 …
如何判断二元一次函数和一元一次函数有没有交点.如题Y=10X-4y=10x^2+4X-20不用求解 2020-06-04 …
现实生活中,乘坐公交车已是人们最平常、最便捷的一种交通方式了。但我们经常看到一些不良现象,诸如乘客 2020-06-17 …