早教吧作业答案频道 -->数学-->
如图,已知四边形ABCD中,AB∥CD,∠ABC=90°,AB=2CD,点P从点A出发以每秒2个单位沿折线AD-DC-CB运动,同时点Q从点A出发以每秒1个单位向点B运动,当其中一个点到达终点时,另一个点也停止运动
题目详情
如图,已知四边形ABCD中,AB∥CD,∠ABC=90°,AB=2CD,点P从点A出发以每秒2个单位沿折线AD-DC-CB运动,同时点Q从点A出发以每秒1个单位向点B运动,当其中一个点到达终点时,另一个点也停止运动,连结PQ、PB,设△PBQ的面积为S,运动时间为t秒,S关于t的大致函数图象如图所示.
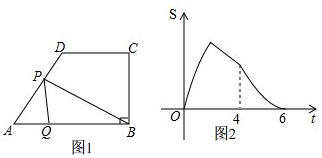
(1)求DC的长;
(2)求出图2中第二段的解析式;
(3)当t为何值时,△PBQ的面积5?

(1)求DC的长;
(2)求出图2中第二段的解析式;
(3)当t为何值时,△PBQ的面积5?
▼优质解答
答案和解析
(1)∵AB=2CD,
∴AD+CD+BC>2AB,
∴点Q先到达终点,由图2,两个点停止时,用了6秒,
∵点Q的运动速度是每秒1个单位,
∴AB=6,
∴DC=3;
(2)如图1,2,
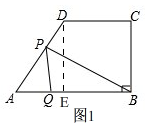
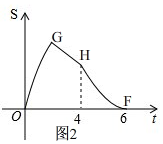
由图2,点P运动4秒时,刚好到达点C,
∴AD+CD=2×4=8,
由(1)知,CD=3,
∴AD=5,
过点D作DE⊥AB于E,
∴BC=DE,
在Rt△ADE中,AE=AB-CD=3,根据勾股定理得,DE=4,
∴BC=4,
∴点P运动5÷2=
秒时,点P到达点D的位置,AQ=
,BQ=AB-AQ=
,
∴S=
BQ•DE=
×
×4=17,
∴G(
,7),
点P运动到点C时,运动时间为4,BQ=AB-AQ=2,
∴S=
BQ×BC=
×2×4=4,
∴H(4,4)
图2中第二段函数是高为BC=4,底BQ逐渐减少,
∴第二段函数是一段线段,
此线段过点G(
,7),H(4,4),
∴图2中第二段的解析式为S=-2t+12(
≤t≤4);
(3)由(2)知,点P在AD上和CD上时,△PBQ=5,
当点P在AD上时,如图3,
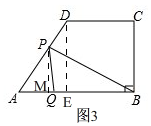
过点D作DE⊥AB于E,过点P作PM⊥AB于M,
在Rt△ADE中,sin∠DAE=
=
,
在Rt△APM中,PM=AP•sin∠DAE=2t×
=
,
BQ=AB-AQ=6-t,
∴S=
BQ•PM=
(6-t)×
=5,
∴t=
(舍)或t=
当点P在CD上时,由(2)知,S=-2t+12,
∴-2t+12=5,
∴t=
;
∴AD+CD+BC>2AB,
∴点Q先到达终点,由图2,两个点停止时,用了6秒,
∵点Q的运动速度是每秒1个单位,
∴AB=6,
∴DC=3;
(2)如图1,2,


由图2,点P运动4秒时,刚好到达点C,
∴AD+CD=2×4=8,
由(1)知,CD=3,
∴AD=5,
过点D作DE⊥AB于E,
∴BC=DE,
在Rt△ADE中,AE=AB-CD=3,根据勾股定理得,DE=4,
∴BC=4,
∴点P运动5÷2=
| 5 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
∴G(
| 5 |
| 2 |
点P运动到点C时,运动时间为4,BQ=AB-AQ=2,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
∴H(4,4)
图2中第二段函数是高为BC=4,底BQ逐渐减少,
∴第二段函数是一段线段,
此线段过点G(
| 5 |
| 2 |
∴图2中第二段的解析式为S=-2t+12(
| 5 |
| 2 |
(3)由(2)知,点P在AD上和CD上时,△PBQ=5,
当点P在AD上时,如图3,

过点D作DE⊥AB于E,过点P作PM⊥AB于M,
在Rt△ADE中,sin∠DAE=
| DE |
| AD |
| 4 |
| 5 |
在Rt△APM中,PM=AP•sin∠DAE=2t×
| 4 |
| 5 |
| 8t |
| 5 |
BQ=AB-AQ=6-t,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 8t |
| 5 |
∴t=
6-
| ||
| 2 |
6-
| ||
| 2 |
当点P在CD上时,由(2)知,S=-2t+12,
∴-2t+12=5,
∴t=
| 7 |
| 2 |
看了 如图,已知四边形ABCD中,...的网友还看了以下:
将数轴上的点A从原点在数轴移动,先向左移动一个长度单位,再向右移动2个单位,又向左移动3个单位,再 2020-05-15 …
已知数轴上点A原点左侧,距原点2个单位长度,点A向右移动12个单位长度到达点B的位置若点P、Q分别 2020-05-15 …
在Rt△ABC中,∠C=90°,AB=10,AC=8,点Q在AB上,且AQ=2,过Q做QR⊥AB, 2020-06-12 …
1将点A(1,-3)向右平移2个单位长度,再向下平移2个单位长度,得到点B(a,b),则ab=多少 2020-06-27 …
一只跳蚤在一条直线上从O点开始起跳,第1次向右跳1个单位,第2次向左跳2个单位,第3次向右跳3个单 2020-06-29 …
(1)一个数乘10,只要把这个数的小数点向()移动()位.(2)把0.325的小数点向右移动一位( 2020-07-19 …
已知直线y=-1/2x+4分别与x轴,y轴交于A·B两点,P从A点出发,以每秒一个单位向原点O运动 2020-07-26 …
如图,等腰梯形ABCD中,AB=CD,AD=2,BC=4.点M从B点出发以每秒2个单位的速度向终点 2020-08-02 …
点P、Q同时从原点出发分别作匀速运动,其中点P沿OA向终点A运动,运动速度为每秒1个单位,点Q沿O 2020-08-02 …
在平面直角坐标系xOy中,有一只电子青蛙在点A(1,0)处.第一次,它从点A先向右跳跃1个单位,再向 2020-11-22 …