早教吧作业答案频道 -->数学-->
(1)如图1,△ABC中,∠C=90°,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为;(2)O是正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.①在图
题目详情
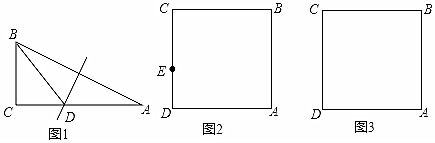
(1)如图1,△ABC中,∠C=90°,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为;
(2)O是正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中作出△EDF,有适当的文字说明,并求出∠EOF的度数;
②若
=
,求
的值.
(2)O是正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中作出△EDF,有适当的文字说明,并求出∠EOF的度数;
②若
| OF |
| OE |
2
| ||
| 3 |
| AF |
| CE |

▼优质解答
答案和解析
(1) ∵AB的垂直平分线交AC于点D,
∵AB的垂直平分线交AC于点D,
∴BD=AD,
∴△BCD的周长=BC+CD+BD=BC+AC=1+2=3,
故答案为:3;
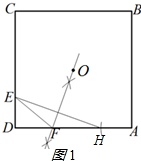
(2)①如图1所示:△EDF即为所求;
如图2所示:AH=DE,
连接OA、OD、OH,
∵点O为正方形ABCD的中心,
∴OA=OD,∠AOD=90°,∠1=∠2=45°,
在△ODE和△OAH中,
,
∴△ODE≌△OAH(SAS),
∴∠DOE=∠AOH,OE=OH,
∴∠EOH=90°,
∵△EDF的周长等于AD的长,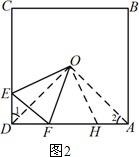
∴EF=HF,
在△EOF和△HOF中,
,
∴△EOF≌△HOF(SSS),
∴∠EOF=∠HOF=45°;
②连接OC,
∵∠ECO=∠EOF=∠OAF=45°,∠EOC=∠AFO,
∴△COE∽△AFO,
∴
=
=
,
∴
•
=
•
∴
=(
)2=(
)2=
.
 ∵AB的垂直平分线交AC于点D,
∵AB的垂直平分线交AC于点D,∴BD=AD,
∴△BCD的周长=BC+CD+BD=BC+AC=1+2=3,
故答案为:3;
(2)①如图1所示:△EDF即为所求;
如图2所示:AH=DE,
连接OA、OD、OH,
∵点O为正方形ABCD的中心,
∴OA=OD,∠AOD=90°,∠1=∠2=45°,
在△ODE和△OAH中,
|
∴△ODE≌△OAH(SAS),
∴∠DOE=∠AOH,OE=OH,
∴∠EOH=90°,
∵△EDF的周长等于AD的长,

∴EF=HF,
在△EOF和△HOF中,
|
∴△EOF≌△HOF(SSS),
∴∠EOF=∠HOF=45°;
②连接OC,
∵∠ECO=∠EOF=∠OAF=45°,∠EOC=∠AFO,
∴△COE∽△AFO,
∴
| AF |
| CO |
| OF |
| OE |
| OA |
| CE |
∴
| AF |
| CO |
| OA |
| CE |
| OF |
| OE |
| OF |
| OE |
∴
| AF |
| CE |
| OF |
| OE |
2
| ||
| 3 |
| 8 |
| 9 |
看了(1)如图1,△ABC中,∠C...的网友还看了以下:
请教高人指导“通常所说的一类连通、三类连通是什么意思请教高人指导“油田开发中,通常所说的一类连通、 2020-05-15 …
你好?想请教大师一个问题,在英文手写时有一个“相靠斜连写”请问是真正的连写吗?相靠斜连写?是直接将 2020-05-16 …
请问,英文书写过程中"直接斜连写""相靠斜连写""直接横连写""相靠横连写"的各自特点.相靠斜连写 2020-05-16 …
求英语连读技巧和规则!还有对于老外说话的疑惑~一直读不好连读,更听不出连读,连读是不是有一定的规则 2020-05-24 …
同济版高数P61的最后一段是什么意思啊?“在区间上每一点都连续的函数,叫做在该区间上连续的函数,或 2020-06-06 …
either..or,neither..nor,notonly..butalso这些连词在句子中的 2020-07-17 …
下面算式的结果是奇数还是偶数?请你连一连。172+256下面算式的结果是奇数还是偶数?请你连一连。 2020-07-18 …
怎么判断一个函数在开区间内是不是连续?是指开区间要是知道一个函数在开区间上是连续的那么在左端点处右 2020-08-01 …
函数在开区间(a,b)上连续是否在开区间(a,b)上一定一致连续?开区间与闭区间的区别若是不能可以 2020-08-01 …
醚键中两边的C上连的必须是三个单键吗?连一个单键和一个双键不可以吗?(就是说如果连了双键的话,还算不 2020-11-03 …