已知，在平面直角坐标系中，AB⊥x轴于点B，点A（a，b）满足a-2b+|b-2|=0，平移线段AB使点A与原点重合，点B的对应点为点C．（1）则a=，b=，点C的坐标为；

Question

已知，在平面直角坐标系中，AB⊥x轴于点B，点A（a，b）满足 √(a-2b)+|b-2|=0，平移线段AB使点A与原点重合，点B的对应点为点C．
（1）则a=___，b=___，点C的坐标为___；
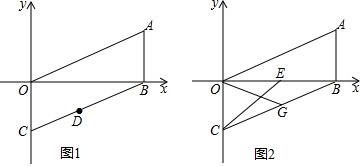
（2）如图1，点D（m，n）在线段BC上，求m，n满足的关系式；
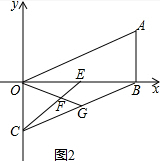
（3）如图2，E是线段OB上一动点，以OB为边作∠BOG=∠AOB，交BC于点G，连CE交OG于点F，若点E在线段OB上运动的过程中， (∠OFC+∠FCG)/(∠OEC)的值是否发生变化？若变化请说明理由，若不变，请求出其值．

Answer 1

（1）∵√(a-2b)+|b-2|=0，√(a-2b)≥0，|b-2|≥0，
∴a-2b=0，b=2，
∴a=4，b=2，
∴AB=BC=2，
∴C（0，-2）．
故答案为4，2，（0，-2）．

（2）如图1中，作DM⊥OB于M，DN⊥OC于N．

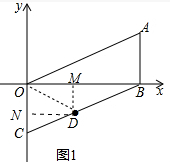
∵B（4，0），C（0，-2），D（m，n），
又∵S_△BOC=S_△OBD+S_△OCD，
∴(1)/(2)•OB•OC=(1)/(2)•OB•DM+(1)/(2)•OC•DN，
∴8=-4n+2m，
∴m-2n=4，
∴m=2n+4．

（3）结论：(∠OFC+∠FCG)/(∠OEC)的值不发生变化．(∠OFC+∠FCG)/(∠OEC)=2．
理由：如图2中，

∵线段OC是由线段AB平移得到，
∴OA∥BC，
∴∠AOB=∠OBG，
∵∠AOB=∠GOB，
∴∠GOB=∠OBG，
∵∠OFC=∠FCG+∠FGC，∠FGC=∠GOB+∠OBG=2∠OBG，
∴∠OFC+∠FCG=2∠FCG+2∠OBG=2（∠ECB+∠EBG），
∵∠OEC=∠ECB+∠EBC，
∴(∠OFC+∠FCG)/(∠OEC)=(2(∠ECB+∠EBC))/(∠ECB+∠EBC)=2．