已知函数g（x）满足g（x）=g（1x），当x∈[13，1]时，g（x）=-3lnx．若函数f（x）=g（x）-mx在区间[13，3]上有三个不同的零点，则实数m的取值范围是（），则实数m的取值范围是（）A.[ln

Question

已知函数g（x）满足g（x）=g（

(1)/(x)），当x∈[(1)/(3)，1]时，g（x）=-3lnx．若函数f（x）=g（x）-mx在区间[(1)/(3)，3]上有三个不同的零点，则实数m的取值范围是（　　），则实数m的取值范围是（　　）

A. [

(ln3)/(3)，(1)/(e)）

B. [ln3，

(3)/(e)）

C. [ln3，

(1)/(e)）

D. （0，

(1)/(e)）

Answer 1

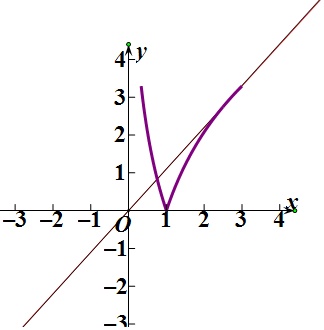∵当x∈[(1)/(3)，1]时，g（x）=-3lnx．
当(1)/(x)∈[(1)/(3)，1]时，x∈[1，3]，
∴g（x）=-3ln(1)/(x)=3lnx
∴g（x）=3|lnx|，x∈[(1)/(3)，3]，
作函数g（x）=3|lnx|与函数y=mx的图象如下
设直线l与f（x）=3|lnx|相切，
如图，设切点为（x，3lnx），
(3lnx)/(x)=(3)/(x)
则由导数的几何意义可得，x=e，
k=(3)/(e)，直线y=(3)/(e)x有2个交点，
当直线y=mx过点（3，3ln3）时有三个交点，
即直线的斜率为ln3，
∴实数m的取值范围：[ln3，(3)/(e)），
故选：B．