早教吧作业答案频道 -->数学-->
已知:△ACB为等腰直角三角形,点P在AC上,连BP,过B点作BE⊥BP,BE=PB,连AE交BC于F.(1)如图1,问PA与CF有何数量关系,并证明;(2)如图2,若点P在CA的延长线上,问上结论是否仍成立,画
题目详情
已知:△ACB为等腰直角三角形,点P在AC上,连BP,过B点作BE⊥BP,BE=PB,连AE交BC于F.
(1)如图1,问PA与CF有何数量关系,并证明;
(2)如图2,若点P在CA的延长线上,问上结论是否仍成立,画图证明.
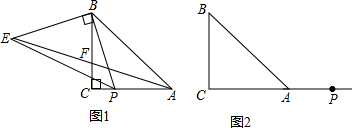
(1)如图1,问PA与CF有何数量关系,并证明;
(2)如图2,若点P在CA的延长线上,问上结论是否仍成立,画图证明.

▼优质解答
答案和解析
(1)结论:PA=2CF,理由如下:
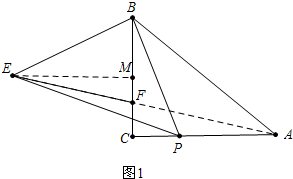 作EM⊥BC垂足为M,
作EM⊥BC垂足为M,
∵∠EBP=∠EMB=90°,
∴∠EBM+∠CBP=90°,∠CBP+∠CPB=90°,
∴∠EBM=∠CPB,
在△EBM和△BPC中,
,
∴△EBM≌△BPC,
∴BM=CP,EM=BC,
∵CB=CA,
∴CM=AP,
∵∠EMC=∠MCA=90°
∴EM∥AC,
∴
=
,
∵EM=BC=AC,
∴MF=FC即MC=2CF,
∴AP=2CF.
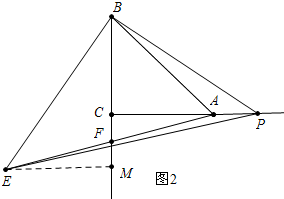
(2)结论不变,如图2,
证明:作EM⊥BC垂足为M,
∵∠EBP=∠EMB=90°,
∴∠EBM+∠CBP=90°,∠CBP+∠CPB=90°,
∴∠EBM=∠CPB,
在△EBM和△BPC中,
,
∴△EBM≌△BPC,
∴BM=CP,EM=BC,∵CB=CA,
∴CM=AP,
∵∠EMC=∠MCA=90°
∴EM∥AC,
∴
=
,
∵EM=BC=AC,
∴MF=FC即MC=2CF,
∴AP=2CF.
 作EM⊥BC垂足为M,
作EM⊥BC垂足为M,∵∠EBP=∠EMB=90°,
∴∠EBM+∠CBP=90°,∠CBP+∠CPB=90°,
∴∠EBM=∠CPB,
在△EBM和△BPC中,
|
∴△EBM≌△BPC,
∴BM=CP,EM=BC,
∵CB=CA,
∴CM=AP,
∵∠EMC=∠MCA=90°
∴EM∥AC,
∴
| EM |
| AC |
| MF |
| CF |

∵EM=BC=AC,
∴MF=FC即MC=2CF,
∴AP=2CF.
(2)结论不变,如图2,
证明:作EM⊥BC垂足为M,
∵∠EBP=∠EMB=90°,
∴∠EBM+∠CBP=90°,∠CBP+∠CPB=90°,
∴∠EBM=∠CPB,
在△EBM和△BPC中,
|
∴△EBM≌△BPC,
∴BM=CP,EM=BC,∵CB=CA,
∴CM=AP,
∵∠EMC=∠MCA=90°
∴EM∥AC,
∴
| EM |
| AC |
| MF |
| CF |
∵EM=BC=AC,
∴MF=FC即MC=2CF,
∴AP=2CF.
看了已知:△ACB为等腰直角三角形...的网友还看了以下:
1.设2的X的4次方减去3的X的立方加上4X加5等于A括号X-1的4次方加上X减1的3次方加上C括 2020-05-13 …
已知函数f(x)=ax+b/x+c(a>0)的图像在点(1,f(1))处的切线方程为y=x-1.( 2020-05-14 …
第一题:设A=(0,1],B=[-1,0],求A∩B第二题:设A={1,2,3,4,5,6,7,8 2020-05-22 …
1.一个质量为50千克的人,它整个身体的体积约是()A.0.005立方米b.0.01立方米c.0. 2020-06-06 …
高中数学已知函数∫(x)=ax平方 bx c已知函数∫(x)=ax平方 bx c(a大于0,bc属 2020-06-27 …
已知函数f(x)=x2+bx+c(b,c∈R﹚.(1)|f﹙1﹚|≤|f﹙-1﹚|≤14成立,求b 2020-07-09 …
.若在A处有20℃的1立方米空气,含有水汽17克,如左图所示已达到饱和.当它上升到C处时有8克水汽 2020-07-10 …
设点P(x,y)是圆(x-3)2+(y-4)2=1上任一点,若不等式x-y+c≤0恒成立,则c的取 2020-07-18 …
X立方-X平方+2X+7表示,或a(x-1)立方+b(x-1)平方+c(x-1)+d,那么abcd 2020-07-22 …
如图,学校的围墙外有一旗杆AB,甲在操场上C处直立3m高的竹竿CD,乙从C处退到E处恰好看到竹竿顶端 2020-10-31 …