早教吧作业答案频道 -->数学-->
在数学学习过程中,我们常常会有“似曾相识”的感觉,如果我们把这些类似进行比较、加以联想的话,可能出现许多意想不到的结果和方法,这种把类似进行比较、联想,从而解决问题的
题目详情
在数学学习过程中,我们常常会有“似曾相识”的感觉,如果我们把这些类似进行比较、加以联想的话,可能出现许多意想不到的结果和方法,这种把类似进行比较、联想,从而解决问题的方法就是类比法.类比法是一种寻求解题思路,猜测问题答案或结论的发现方法.
如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.
【尝试探索】
①经过三角形顶点的面积等分线有___条;
②平行四边形有___条面积等分线.
【类比探究】
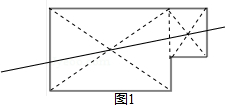
如图1所示,在矩形中剪去一个小正方形,请画出这个图形的一条面积等分线;
【类比拓展】
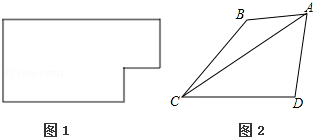
如图2,四边形ABCD中,AB与CD不平行,AB≠CD,且S△ABC<S△ACD,过点A画出四边形ABCD的面积等分线,并描述方法.
【灵活运用】
请您尝试画出一种图形,并画出它的一条面积等分线.
如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.

【尝试探索】
①经过三角形顶点的面积等分线有___条;
②平行四边形有___条面积等分线.
【类比探究】
如图1所示,在矩形中剪去一个小正方形,请画出这个图形的一条面积等分线;
【类比拓展】
如图2,四边形ABCD中,AB与CD不平行,AB≠CD,且S△ABC<S△ACD,过点A画出四边形ABCD的面积等分线,并描述方法.
【灵活运用】
请您尝试画出一种图形,并画出它的一条面积等分线.
▼优质解答
答案和解析
 尝试探索,①三角形的三条中线是面积等分线,
尝试探索,①三角形的三条中线是面积等分线,
∴经过三角形顶点的面积等分线有3条,
②∵平行四边形的中心对称图形,
∴经过对称中心的直线都是它的面积等分线,
∴平行四边形有无数条面积等分线,
故答案为:3;无数;
类比探究,如图1所示,经过两个矩形对角线的交点的直线是这个图形的一条面积等分线;
类比拓展,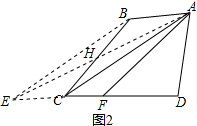 如图2,
如图2,
过点B作BE∥AC交DC的延长线于点E,连接AE交BC于F,
∵△ABC和△AEC的公共边AC上的高也相等,
∴S△ABC=S△AEC,
∴S△ABH=S△HEC,
∴四边形ABCD的面积=△AED的面积,
∴△AED的中线AF是四边形ABCD的面积等分线;
灵活运用,如图3,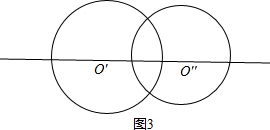
经过两圆圆心的直线O′O′′是这个图形的面积等分线.
 尝试探索,①三角形的三条中线是面积等分线,
尝试探索,①三角形的三条中线是面积等分线,∴经过三角形顶点的面积等分线有3条,
②∵平行四边形的中心对称图形,
∴经过对称中心的直线都是它的面积等分线,
∴平行四边形有无数条面积等分线,
故答案为:3;无数;
类比探究,如图1所示,经过两个矩形对角线的交点的直线是这个图形的一条面积等分线;
类比拓展,
 如图2,
如图2,过点B作BE∥AC交DC的延长线于点E,连接AE交BC于F,
∵△ABC和△AEC的公共边AC上的高也相等,
∴S△ABC=S△AEC,
∴S△ABH=S△HEC,
∴四边形ABCD的面积=△AED的面积,
∴△AED的中线AF是四边形ABCD的面积等分线;
灵活运用,如图3,

经过两圆圆心的直线O′O′′是这个图形的面积等分线.
看了在数学学习过程中,我们常常会有...的网友还看了以下:
翻译英语,她似乎是有意地做这些事.2.他们为自己属于这么好的一个团队而自豪.3.他表现地就像没发生 2020-04-07 …
人们将要像用镰刀割草似的把我们消灭掉.这是一个比喻句把比作. 2020-05-14 …
怎么理解这句话?似乎很有人生哲理生命并不比一头烟头延续的更为长久,而命运却把我们像敲落烟灰似的给敲 2020-05-16 …
y=f(x)在[a,b]上连续非负,由曲线f(x),直线x=a,x=b及x轴围城的平面绕y轴旋转一 2020-05-16 …
关于实现梦想激励的一段话60-80字不要说遇到了困难不要放弃类似的话,而是在开始“梦想之旅”前的激 2020-05-24 …
卖炭翁与.石壕吏的类似的句子卖炭翁一诗通过把,称,叱,牵几个简洁而有力的动词,描绘出宫使如狼似虎的 2020-06-06 …
寒冬春暖这篇文章作者要告诉人们什么道理?鹅毛大雪漫天飞舞,凛冽的北风呼啸而来……突然脚下一滑,我跪 2020-06-08 …
把下面的名言补充完整,并且再写一句人非生而知之者,----------------?一鼓作气,-- 2020-06-10 …
答对给你56分..一定那是力争上游的一种树,笔直的干,笔直的枝.它的干呢,通常是丈把高,像是加以人 2020-06-15 …
与寻寻觅觅相似的词.而且要是动词! 2020-06-18 …