早教吧作业答案频道 -->数学-->
如图,P是菱形ABCD所在平面外一点,∠BAD=60°,△PCD是等边三角形,AB=2,PA=22,M是PC的中点,点G为线段DM上一点(端点除外),平面APG与BD交于点H.(Ⅰ)求证:PA∥GH;(Ⅱ)求证:平面PAC
题目详情
如图,P是菱形ABCD所在平面外一点,∠BAD=60°,△PCD是等边三角形,AB=2,PA=2
,M是PC的中点,点G为线段DM上一点(端点除外),平面APG与BD交于点H.
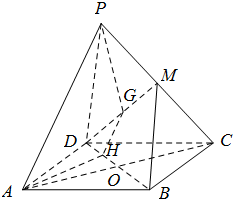
(Ⅰ)求证:PA∥GH;
(Ⅱ)求证:平面PAC⊥平面BDM;
(Ⅲ)求几何体M-BDC的体积.
| 2 |

(Ⅰ)求证:PA∥GH;
(Ⅱ)求证:平面PAC⊥平面BDM;
(Ⅲ)求几何体M-BDC的体积.
▼优质解答
答案和解析
(I)证明:连接MO.
∵四边形ABCD是菱形,∴O为AC的中点,
∵点M为PC的中点,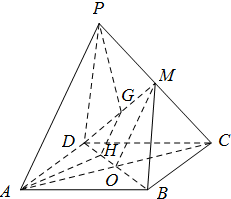
∴MO∥PA.
又MO⊂平面BDM,PA⊄平面BDM,
∴PA∥平面BDM.
又∵平面APG∩平面平面BDM=GH,PA⊂平面APG,
∴PA∥GH.
(II)证明:∵△PCD是边长为2的等边三角形,M是PC的中点.
∴DM=
.
∵四边形ABCD是菱形,AB=2,∠BAD=60°,
∴△ABD是边长为2的等边三角形,∴DO=
BD=1,
又MO=
PA=
,
∴DO2+MO2=DM2,∴BD⊥MO.
∵菱形ABCD中,BD⊥AC,
又MO⊂平面PAC,AC⊂平面PAC,MO∩AC=O,
∴BD⊥平面PAC.
又BD⊂平面BDM,
∴平面PAC⊥平面BDM.
(III) ∵四边形ABCD是菱形,∠BAD=60°,AB=2,
∴AC=2AO=2
.
在△PAC中,∵PA=2
,AC=2
,PC=2,
∴PA2+PC2=AC2,
∴PA⊥PC,∵MO∥PA,
∴PC⊥MO,
又平面PAC⊥平面BDM,平面PAC∩平面BDM=MO,PC⊂平面PAC,
∴PC⊥平面BDM.
∴VM-BDC=VC-BDM=
S△BDM•CM=
×
×BD×MO×MC=
×
×2×
×1=
.
∵四边形ABCD是菱形,∴O为AC的中点,
∵点M为PC的中点,

∴MO∥PA.
又MO⊂平面BDM,PA⊄平面BDM,
∴PA∥平面BDM.
又∵平面APG∩平面平面BDM=GH,PA⊂平面APG,
∴PA∥GH.
(II)证明:∵△PCD是边长为2的等边三角形,M是PC的中点.
∴DM=
| 3 |
∵四边形ABCD是菱形,AB=2,∠BAD=60°,
∴△ABD是边长为2的等边三角形,∴DO=
| 1 |
| 2 |
又MO=
| 1 |
| 2 |
| 2 |
∴DO2+MO2=DM2,∴BD⊥MO.
∵菱形ABCD中,BD⊥AC,
又MO⊂平面PAC,AC⊂平面PAC,MO∩AC=O,
∴BD⊥平面PAC.
又BD⊂平面BDM,
∴平面PAC⊥平面BDM.
(III) ∵四边形ABCD是菱形,∠BAD=60°,AB=2,
∴AC=2AO=2
| 3 |
在△PAC中,∵PA=2
| 2 |
| 3 |
∴PA2+PC2=AC2,
∴PA⊥PC,∵MO∥PA,
∴PC⊥MO,
又平面PAC⊥平面BDM,平面PAC∩平面BDM=MO,PC⊂平面PAC,
∴PC⊥平面BDM.
∴VM-BDC=VC-BDM=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| ||
| 3 |
看了如图,P是菱形ABCD所在平面...的网友还看了以下:
已知化合物NH5的结构和NH4Cl相似,下列关于NH5的下列说法中正确的是()A.NH5是共价化合 2020-05-13 …
(1)常温下,0.1mol•L-1的CH3COOH溶液加水稀释过程中,下列表达式的数据变大的是(填 2020-05-14 …
已知室温时,0.1mo1/L某一元酸HA在水中有0.1%发生电离,下列叙述错误的是()A.该溶液的 2020-05-14 …
将0.2mol/LCH3COONa溶液与0.1mol/L盐酸等体积混合,混合溶液中下列微粒的物质的 2020-05-16 …
将0.2mol/L CH3COOK与0.1mol/L盐酸等体积混合后,溶液中下列微粒的物质的量浓度 2020-05-16 …
【高考】将0.2mol/LCH3COOK与0.1mol/L盐酸等体积混合,溶液中下列微粒物质的量的 2020-05-16 …
为什么氢根不可大于阴离子是2010年正定中学月考的一道题:已知一溶液中有4种离子:X+Y-H+OH 2020-05-22 …
已知某温度下,在100mL浓度为0.01mol/L的NaHB强电解质溶液中,c(H+)>c(H―) 2020-05-24 …
化学电离选择题选择题:当不考虑水的电离时,在氢硫酸溶液中,下列的离子浓度关系中正确的是()A.c( 2020-06-04 …
在0.1mol/L的NaCO3溶液中,下列关系是正确的是Ac(Na+)>c(HCO3-)>c(CO3 2020-12-12 …