某菜农有两段总长度为20米的篱笆PA及PB，现打算用它们和两面成直角的墙OM、ON围成一个如图所示的四边形菜园OAPB（假设OM、ON这两面墙都足够长）．已知|PA|=|PB|=10（米），∠AOP=∠BOP=π4，∠OA

Question

某菜农有两段总长度为20米的篱笆PA及PB，现打算用它们和两面成直角的墙OM、ON围成一个如图所示的四边形菜园OAPB（假设OM、ON这两面墙都足够长）．已知|PA|=|PB|=10（米），∠AOP=∠BOP=(π)/(4)，∠OAP=∠OBP．设∠OAP=θ，四边形OAPB的面积为S．

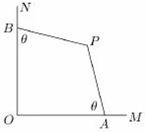
（1）将S表示为θ的函数，并写出自变量θ的取值范围；
（2）求出S的最大值，并指出此时所对应θ的值．

Answer 1

（1）在三角POB中，由正弦定理，得：OBsin(3π4-θ)=10sinπ4，得OB=10（cosθ+sinθ）．所以，S=2×12×10×10(cosθ+sinθ)sinθ=100（sinθcosθ+sin2θ），θ∈(0，π4)∪(π4，3π4)．（2）S=100（sinθcosθ+s...