早教吧作业答案频道 -->数学-->
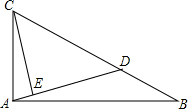
如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=12,BC=3BD,CE⊥AD,则AECE=.
题目详情
如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=
,BC=3BD,CE⊥AD,则
=___.
| 1 |
| 2 |
| AE |
| CE |

▼优质解答
答案和解析
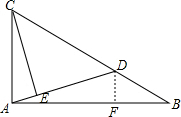 过点D作DF⊥AB于点F,
过点D作DF⊥AB于点F,
∵∠CAB=90°,DF⊥AB,
∴AC∥DF,
∴
=
=
∵BC=3BD,
∴
=
=
,
∴AF=k•BF
∵tanB=
,
∴
=
,
∴DF=
FB,
∴
=
=
,
∵CE⊥AD,
∴tan∠ACE=
,
∵∠CAE+∠ACE=90°,∠CAE+∠DAB=90°,
∴∠ACE=∠DAF,
∴tan∠ACE=tan∠DAF=
=
.
故答案为:
.
 过点D作DF⊥AB于点F,
过点D作DF⊥AB于点F,∵∠CAB=90°,DF⊥AB,
∴AC∥DF,
∴
| BD |
| DC |
| BF |
| AF |
∵BC=3BD,
∴
| BD |
| DC |
| BF |
| AF |
| 1 |
| 2 |
∴AF=k•BF
∵tanB=
| 1 |
| 2 |
∴
| DF |
| FB |
| 1 |
| 2 |
∴DF=
| 1 |
| 2 |
∴
| DF |
| AF |
| ||
| AF |
| 1 |
| 4 |
∵CE⊥AD,
∴tan∠ACE=
| AE |
| EC |
∵∠CAE+∠ACE=90°,∠CAE+∠DAB=90°,
∴∠ACE=∠DAF,
∴tan∠ACE=tan∠DAF=
| AE |
| EC |
| DF |
| AF |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
看了 如图,已知点D是Rt△ABC...的网友还看了以下:
关于质点做匀速圆周运动的说法正确的是A.由a=v2/r知a与r成反比B.由a=ω2r知a与r成正比 2020-04-12 …
高中的物理有关向心力的问题关于质点做匀速圆周运动,下列说法正确的是()A.由a=v^2/r知a与r 2020-04-26 …
关于质点做匀速圆周运动的下列说法中正确的是()A.由a=v2/r知a与r成反比B.由a=ω2r知a 2020-05-13 …
假定有两个关系R与S,其内容分别为:R关系 S关系ABCBCD12525 1725625935454 2020-05-24 …
假定有两个关系R与S,其内容分别为:R关系S关系ABCBCD1252517256259354541( 2020-05-24 …
设矩阵,为阶方阵,满足等式,则下列关于矩阵秩的论述正确的是().A.R(A)>=R(C)B.R(B 2020-06-18 …
证明:b1b2b3可由a1a2线性表出则b1b2b3线性相关B=[b1b2b3];A=[a1a2] 2020-07-09 …
对于函数f(x)=asinx+bx+c(其中,a,b∈R,c∈Z),选取a,b,c的一组值计算f( 2020-07-09 …
已知函数fx=ax^2+bx+c(a>0,b∈R,c∈R)已知函数f(x)=ax^2+bx+c(a 2020-07-26 …
已知关系模式R=(A,B,C,D,E,F,G)满足.求R的码已知关系模式R=(A,B,C,D,E,F 2020-11-19 …