已知Rt△ABC，斜边BC⊊α，点A∈α，AO⊥α，O为垂足，∠ABO=30°，∠ACO=45°，求二面角A-BC-O的大小．

Question

已知Rt△ABC，斜边BC⊊α，点A∈α，AO⊥α，O为垂足，∠ABO=30°，∠ACO=45°，求二面角A-BC-O的大小．

Answer 1

如图，在平面α内，过O作OD⊥BC，垂足为D，连结AD，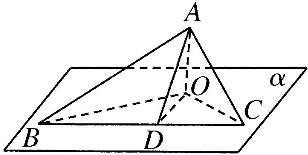
设OC=a，∵AO⊥α，BC⊂α，
∴AO⊥BC，又∵AO∩OD=O，∴BC⊥平面AOD，
∵AD⊂平面AOD，∴AD⊥BC，
∴∠ADO是二面角A-BC-O的平面角，
∵AO⊥α，OB⊂α，OC⊂α，∴AO⊥OB，AO⊥OC，
又∠ABO=30°，∠ACO=45°，∴AO=a，AC=√(2)a，AB=2a，
在Rt△ABC中，∠BAC=90°，
∴BC=√(AC2+AB2)=√(6)a，∴AD=(AB•AC)/(BC)=(2a•√(2)a)/(√(6)a)=(2√(3))/(3)a，
在Rt△AOD中，sin∠ADO=(AO)/(AD)=(a)/((2√(3))/(3)a)=(√(3))/(2)，
∴∠ADO=60°．
∴二面角A-BC-O的大小是60°．