早教吧作业答案频道 -->数学-->
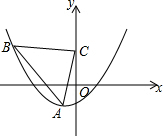
已知,抛物线y=18(x+1)2-2顶点为A,点B在抛物线上,以AB的斜边作等腰直角三角形,直角顶点C在y轴上,求C点坐标.
题目详情
已知,抛物线y=
(x+1)2-2顶点为A,点B在抛物线上,以AB的斜边作等腰直角三角形,直角顶点C在y轴上,求C点坐标.
| 1 |
| 8 |

▼优质解答
答案和解析
 ∵抛物线y=
∵抛物线y=
(x+1)2-2顶点为A,
∴A(-1,-2),
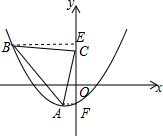
作BE⊥y轴于E,AF⊥y轴于F,
∵△ABC是以AB的斜边等腰直角三角形,
∴AC=BC,∠ACB=90°,
∴∠BCE+∠ACF=90°,
∵∠BCE+∠EBC=90°,
∴∠ACF=∠EBC,
在△ACF和△CBE中
∴△ACF≌△CBE(AAS),
∴AF=CE,CF=BE,
设C(0,n),则BE=CF=n+2,AF=CE=1,
∴B(-n-2,n+1),
∵点B在抛物线上,
∴n+1=
(-n-2+1)2-2,
解得n=3±4
,
∴C(0,3+4
)或(0,3-4
).
 ∵抛物线y=
∵抛物线y=| 1 |
| 8 |
∴A(-1,-2),
作BE⊥y轴于E,AF⊥y轴于F,
∵△ABC是以AB的斜边等腰直角三角形,
∴AC=BC,∠ACB=90°,
∴∠BCE+∠ACF=90°,
∵∠BCE+∠EBC=90°,
∴∠ACF=∠EBC,
在△ACF和△CBE中
|
∴△ACF≌△CBE(AAS),
∴AF=CE,CF=BE,
设C(0,n),则BE=CF=n+2,AF=CE=1,
∴B(-n-2,n+1),
∵点B在抛物线上,
∴n+1=
| 1 |
| 8 |
解得n=3±4
| 2 |
∴C(0,3+4
| 2 |
| 2 |
看了 已知,抛物线y=18(x+1...的网友还看了以下:
已知等腰三角形一腰上的高与另一腰的夹角为45°,则这个等腰三角形的顶角读书时多少?直线y=x-1与 2020-05-13 …
一个锐角三角形ABC,A是上面的顶点,B是左侧的顶点,C是右侧的顶点.以AB边为一腰向该三角形外做 2020-05-22 …
下列叙述正确的是:A有两边和一角对应相等的两个三角形全等;B有一腰相等的两个等腰三角形全等;C有一 2020-06-06 …
在三角形abc中,若c角为60度,则a除以b+c与b除以c+a的和是多少的解法 2020-06-07 …
1.要画一个三角形,需要知道三个元素,其中至少一个元素是2.三角形的三边长a,b,c,满足b分之a 2020-06-08 …
已知钝角△ABC的面积为3√3,BC=4,CA=3,则C角为多少度?要详细步骤哇,谢了速度出答案哇 2020-07-15 …
下列命题是否正确1.若△ABC的三边a、b、c满足a2+b2+c2+338=10a+24b+26c 2020-07-19 …
下列四组图案中不一定相似的是A、各有一个角为40度的两个等腰三角形B、两个等腰直角三角形C、有一个 2020-07-30 …
判断哪个是全等三角形(1)A各有一个角为45度的两个等腰三角形B两个等边三角形C各有一个角是40度 2020-08-03 …
在△ABC中,角A,B,C的对边分别为a,b,c,其中c边最长,并且sin2A+sin2B=1,则 2020-08-03 …