早教吧作业答案频道 -->数学-->
(理科)定义在R上的函数是奇函数,当且仅当x=1时,f(x)取得最大值.(1)求a、b的值;(2)若方程上有且仅有两个不同实根,求实数m的取值范围.
题目详情
(理科)定义在R上的函数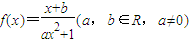 是奇函数,当且仅当x=1时,f(x)取得最大值.
是奇函数,当且仅当x=1时,f(x)取得最大值.
(1)求a、b的值;
(2)若方程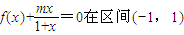 上有且仅有两个不同实根,求实数m的取值范围.
上有且仅有两个不同实根,求实数m的取值范围.
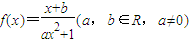 是奇函数,当且仅当x=1时,f(x)取得最大值.
是奇函数,当且仅当x=1时,f(x)取得最大值.(1)求a、b的值;
(2)若方程
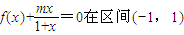 上有且仅有两个不同实根,求实数m的取值范围.
上有且仅有两个不同实根,求实数m的取值范围.▼优质解答
答案和解析
分析:
(1)利用奇函数的定义f(-x)=-f(x)得b=0,通过对x的分段讨论求出函数的最大值,根据已知条件得到关于a的方程,求出a的值.(2)将f(x)代入方程并将方程变形,将方程根的情况转换为二次方程的实根分布问题,结合二次函数的图象写出限制条件,求出m的范围.
(1)由f(-x)=-f(x)得b=0∴又由函数f(x)的定义域为R知a≥0当且仅当ax2=1即∴综上a=1,b=0…(6分)(2)∴方程mx2+x+m+1=0在区间(-1,1)上有且仅有一个非零实根.当m=0时,x=-1不合题意当m≠0时,分两种情况讨论①②令h(x)=mx2+x+m+1则h(-1)•h(1)<0且h(0)≠0解得-1<m<0综上所述实数m的取值范围为…(13分)
点评:
本题考查二次方程的实根分布问题,应该结合二次函数的图象,从对称轴与区间的位置关系、区间端点值的符号限制.
分析:
(1)利用奇函数的定义f(-x)=-f(x)得b=0,通过对x的分段讨论求出函数的最大值,根据已知条件得到关于a的方程,求出a的值.(2)将f(x)代入方程并将方程变形,将方程根的情况转换为二次方程的实根分布问题,结合二次函数的图象写出限制条件,求出m的范围.
(1)由f(-x)=-f(x)得b=0∴又由函数f(x)的定义域为R知a≥0当且仅当ax2=1即∴综上a=1,b=0…(6分)(2)∴方程mx2+x+m+1=0在区间(-1,1)上有且仅有一个非零实根.当m=0时,x=-1不合题意当m≠0时,分两种情况讨论①②令h(x)=mx2+x+m+1则h(-1)•h(1)<0且h(0)≠0解得-1<m<0综上所述实数m的取值范围为…(13分)
点评:
本题考查二次方程的实根分布问题,应该结合二次函数的图象,从对称轴与区间的位置关系、区间端点值的符号限制.
看了(理科)定义在R上的函数是奇函...的网友还看了以下:
1.若函数y=f(x)的值域为[3,10],则函数y=f(x-1)的值域为,函数y=f(x)-1的 2020-04-06 …
已知二次函数过点(1,0)(3,0)且其最小值为-6求1函数的解析式2写出其单调区间3若-4≤x≤ 2020-04-26 …
已知函数f(x)=3^x,f(a+2)=27,函数g(x)=λ·2^ax-4^x的定义域为[0,2 2020-04-27 …
已知:二次函数y=ax²+bx+c的图像经过A(﹣1,0),B(4,0),C(0,k)三点,其中∠ 2020-05-16 …
设3阶实对称矩阵A的秩为2,λ1=λ2=6是A的二重特征值,若α1=(1,1,0)^T,α2=(2 2020-06-30 …
已知函数f(x)=lnx-a/x-x+3(a∈R)(1)若函数在x=2处取得极值,求实数a的值,并 2020-07-31 …
已知函数y=x3+3px2+3px+1(1)试问该函数能否在x=-1处取到极值?若有可能,求实数p 2020-08-01 …
某学生对函数f(x)=sinxsin11x进行研究后,得出如下结论:①函数f(x)是偶函数②函数f( 2020-10-31 …
若1/m-1/n=3,求2m-3mn-2n/m-2mn-m的值以知xyz不等于0且x+3y+7z=0 2020-10-31 …
求函数的值域1,函数y=sinx(π/6≤x≤2π/3)的值域是?为什么是[1/2,1]π/6和2π 2021-02-18 …