早教吧作业答案频道 -->数学-->
阅读理如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,若这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相
题目详情
阅读理 如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,若这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.解决问题.
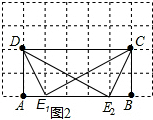
(1)如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(2)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.
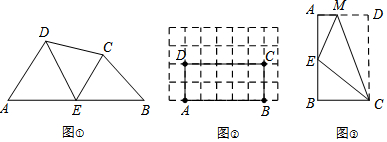
(1)如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(2)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.

▼优质解答
答案和解析
(2)如图所示:点E是四边形ABCD的边AB上的强相似点,
(3)结论:BC=
AB.
理由:如图③中,
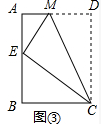
∵点E是四边形ABCM的边AB上的一个强相似点,
∴△AEM∽△BCE∽△ECM,
∴∠BCE=∠ECM=∠AEM.
由折叠可知:△ECM≌△DCM,
∴∠ECM=∠DCM,CE=CD,
∴∠BCE=
∠BCD=30°,
BE=
CE=
AB.
∴点E是AB的中点时,点E恰好是四边形ABCM的边AB上的一个强相似点,
设AE=BE=a,则EC=2a,
在Rt△EBC中,BC=
=
a,
∴AB:BC=2a:
a=2:
,
∴BC=
AB.

(3)结论:BC=
| ||
| 2 |
理由:如图③中,

∵点E是四边形ABCM的边AB上的一个强相似点,
∴△AEM∽△BCE∽△ECM,
∴∠BCE=∠ECM=∠AEM.
由折叠可知:△ECM≌△DCM,
∴∠ECM=∠DCM,CE=CD,
∴∠BCE=
| 1 |
| 3 |
BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴点E是AB的中点时,点E恰好是四边形ABCM的边AB上的一个强相似点,
设AE=BE=a,则EC=2a,
在Rt△EBC中,BC=
| EC2-EB2 |
| 3 |
∴AB:BC=2a:
| 3 |
| 3 |
∴BC=
| ||
| 2 |
看了阅读理如图①,在四边形ABCD...的网友还看了以下:
四边形对角线与四边形面积有什么关系 2020-04-25 …
《初中数学与式精练800题》答案后面本来是有答案的.被我妈狠心地撕了~求好人截个图、或者用其它办法 2020-06-19 …
如图,△ABE与△ACD都是等边三角形,△AEC旋转后能与△ABD重合,EC与BD相交于点F,求如 2020-06-27 …
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=23,E是 2020-07-18 …
如图m是平行四边形的边AB的中点,CM与BD相交于点E,求三角形与四边形的比A在左下角,B在右下角 2020-07-30 …
三角形的中位线分这个三角形所成的小三角形与四边形的面积之比为. 2020-08-01 …
三角形的中位线分这个三角形所成的小三角形与四边形的面积之比为. 2020-08-01 …
(2004•静安区二模)三角形的中位线分这个三角形所成的小三角形与四边形的面积之比为. 2020-12-16 …
已知△ABC,如图,如果要作与BC平行的直线把△ABC划分成两部分,使这两部分(三角形与四边形)的面 2020-12-17 …
如图①,用两个全等的等边三角形△ABC和△ACD拼成四边形ABCD,把一个含60°角的三角尺与四边形 2020-12-17 …