已知函数f（x）=x3，x≤ax2，x>a.若存在实数b，使函数g（x）=f（x）-b有两个零点，则a的取值范围是（）A.（-∞，-1）∪（0，+∞）B.（-∞，0）∪（1，+∞）C.（-∞，0）D.（0，1）

Question

已知函数f（x）=

x3，x≤a

x2，x>a.

若存在实数b，使函数g（x）=f（x）-b有两个零点，则a的取值范围是（　　）

A. （-∞，-1）∪（0，+∞）

B. （-∞，0）∪（1，+∞）

C. （-∞，0）

D. （0，1）

Answer 1

∵g（x）=f（x）-b有两个零点，
∴f（x）=b有两个零点，即y=f（x）与y=b的图象有两个交点，
由x³=x²可得，x=0或x=1
①当a>1时，函数f（x）的图象如图所示，此时存在b，满足题意，故a>1满足题意

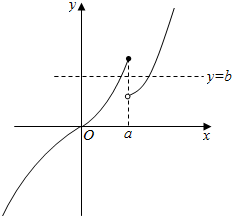
②当a=1时，由于函数f（x）在定义域R上单调递增，故不符合题意
③当0
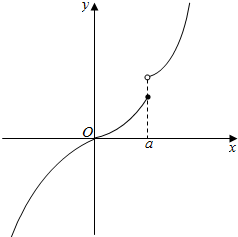
④a=0时，f（x）单调递增，故不符合题意
⑤当a<0时，函数y=f（x）的图象如图所示，此时存在b使得，y=f（x）与y=b有两个交点

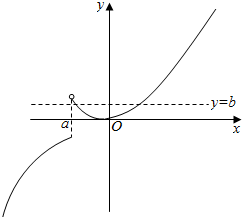
综上可得，a<0或a>1
则a的取值范围是（-∞，0）∪（1，+∞），
故选：B．