早教吧作业答案频道 -->数学-->
设计一水槽,其横截面为等腰梯形,要求AB+BC+CD=3∠ABC=120°.(1)写出横截面面积S用腰长为x表示的函数关系式,并求出定义域;(2)问当腰长为多少时,横截面面积最大?最大值是多
题目详情
设计一水槽,其横截面为等腰梯形,要求AB+BC+CD=3 ∠ABC=120°.
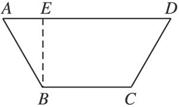
(1)写出横截面面积S用腰长为x表示的函数关系式,并求出定义域;
(2)问当腰长为多少时,横截面面积最大?最大值是多少?
▼优质解答
答案和解析
(1)设AB=CD=x,则BC=3-2x.又作BE⊥AD于E. ∵∠ABC=120° ∴∠BAE=60°.∴BE= x AE= AD=BC+2AE=3-2x+x=3-x. ∴S= (AD+BC)·BE = (3-x+3-2x)· x=- x. ∵AB>0 BC>0 ∴ ∴0<x< 即定义域为(0, ...
看了 设计一水槽,其横截面为等腰梯...的网友还看了以下:
反比函数题已知反比函数y=8/x上有2点A(2.4)B(4,2),做AC垂直于X轴,BD垂直于x轴, 2020-03-31 …
一个长方形的长是a厘米,宽是b厘米.(1)写出它的面积计算公式(面积为S).如果a=7.5,b=3 2020-05-13 …
一个长方形的长是a厘米,宽是b厘米.(1)写出它的面积计算公式(面积为S).如果a=7.5,b=3 2020-05-13 …
如图,有一块半径为2的半圆形钢板,计划剪裁成矩形ABCD的形状,设AD=x,矩形ABCD的面积为y 2020-05-14 …
y=x^2在(1,1)处的切线L与曲线C及X轴围成的封闭图形的面积切线方程求出是Y=2X-1然后我 2020-05-16 …
若矩形的长是4cm,宽是3cm,如果将其长与宽都增加xcm,那么面积增加ycm^2,1.写出y与x 2020-05-16 …
用60m的篱笆围成矩形,使矩形一边靠墙,另三边用篱笆围成,1.写出矩形面积s(m?)与平行于墙的一 2020-06-16 …
求出抛物线Y=1-X^2及其在点(1,0)处得切线和Y轴所谓的平面图形得面积.求出上述图形绕X轴旋 2020-07-31 …
1.已知a+b=-2,则a^2+ab+2a=2.若非零实数a、b满足4a^2-4ab+b^2=0,则 2020-12-07 …
ab是函数y=1/x的图像上关于原点o对称的任意两点ac平形于y轴bc平形于x轴若点a的坐标为(1, 2021-02-14 …