早教吧作业答案频道 -->数学-->
如图,AB是O的直值,CD为弦,AE⊥CD于E,BF⊥CD于F.(1)试判断线段DF和CE的数量关系,并说明理由.(2)若AB=10,AE=3,BF=5,求EF和EC的长.
题目详情
如图,AB是 O的直值,CD为弦,AE⊥CD于E,BF⊥CD于F.
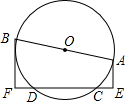
(1)试判断线段DF和CE的数量关系,并说明理由.
(2)若AB=10,AE=3,BF=5,求EF和EC的长.

(1)试判断线段DF和CE的数量关系,并说明理由.
(2)若AB=10,AE=3,BF=5,求EF和EC的长.
▼优质解答
答案和解析
(1)DF=CE,
理由是:如图1,过O作OQ⊥EF于Q,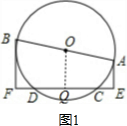
∵AE⊥CD,BF⊥CD,
∴BF∥OQ∥AE,
∵BO=AO,
∴QF=QE,
∵OQ⊥DC,OQ过O,
∴DQ=CQ,
∴QF-DQ=QE-CQ,
∴DF=CE;
(2) 如图2,过A作AM∥EF交BF于M,交OQ于N,连接OD,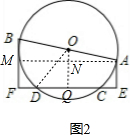
∵AB=10,AE=3,BF=5,
∴BM=5-3=2,
由勾股定理得:EF=AM=
=4
,
∴AN=QE=FQ=2
,
在Rt△AON中,ON=
=
=1,
∴OQ=2+1=3,
在Rt△OQD中,由勾股定理得:DQ=
=
=4,
∴EC=DF=QF-DQ=2
-4.
理由是:如图1,过O作OQ⊥EF于Q,

∵AE⊥CD,BF⊥CD,
∴BF∥OQ∥AE,
∵BO=AO,
∴QF=QE,
∵OQ⊥DC,OQ过O,
∴DQ=CQ,
∴QF-DQ=QE-CQ,
∴DF=CE;
(2) 如图2,过A作AM∥EF交BF于M,交OQ于N,连接OD,

∵AB=10,AE=3,BF=5,
∴BM=5-3=2,
由勾股定理得:EF=AM=
| 102-22 |
| 6 |
∴AN=QE=FQ=2
| 6 |
在Rt△AON中,ON=
| OA2-AN2 |
52-(2
|
∴OQ=2+1=3,
在Rt△OQD中,由勾股定理得:DQ=
| OD2-OQ2 |
| 52-32 |
∴EC=DF=QF-DQ=2
| 6 |
看了如图,AB是O的直值,CD为弦...的网友还看了以下:
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,并且a,b是方程x2-x- 2020-06-03 …
··一道简单的数学题,先到的.对的.角D=90度,BD=CD,BO是角DBC的角平分线,CE垂直B 2020-06-03 …
如图,A,P,B,C是⊙O上的四点,∠APC=∠BPC=60°猜想pa pb pc三者间的数量关系 2020-06-27 …
△ABC中,角ABC所对的变分别为a,b,c,点O满足aOA+bOB+cOC=0,则动点O的轨迹一 2020-07-22 …
已知菱形ABCD的对角线交于点O,AC=6,BD=8,以A为圆心,r为半径画⊙A,对于B,C,D, 2020-07-26 …
向量练习,救命啊,1,平行四边形ABCD中,对角线AC与BD相交于点O,在以A,B,C,D,O中的 2020-07-30 …
已知集合A{1,2},集合B{x|x属于A},集合C{x|x是A的子集},试用列举法写出集合B,C 2020-08-01 …
已知正方体ABCDA'B'C'D',O是底ABCD对角线的交点,求证:(1)C'O//面AB'D'( 2020-11-02 …
设A,B均为n阶方阵,且满足AB=Θ(零矩阵),则必有()A.A=Θ或B=ΘB.A+B=ΘC.|A| 2020-11-02 …
这几个字母怎么拼才是单词呢?B-E-E-N-M-O-R-VA-E-R-T-WA-B-C-D-O-P- 2021-02-09 …