早教吧作业答案频道 -->数学-->
若直角坐标平面内的两个不同点M、N满足条件:①M、N都在函数y=f(x)的图象上;②M、N关于原点对称.则称点对[M,N]为函数y=f(x)的一对“友好点对”.(注:点对[M,N]与[N,M]为
题目详情
若直角坐标平面内的两个不同点M、N满足条件:
①M、N都在函数y=f(x)的图象上;
②M、N关于原点对称.则称点对[M,N]为函数y=f(x)的一对“友好点对”.(注:点对[M,N]与[N,M]为同一“友好点对”),已知函数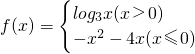 ,此函数的“友好点对”有________.
,此函数的“友好点对”有________.
①M、N都在函数y=f(x)的图象上;
②M、N关于原点对称.则称点对[M,N]为函数y=f(x)的一对“友好点对”.(注:点对[M,N]与[N,M]为同一“友好点对”),已知函数
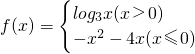 ,此函数的“友好点对”有________.
,此函数的“友好点对”有________.▼优质解答
答案和解析
2个
分析:
根据题意:“友好点对”,可知,欲求f(x)的“友好点对”,只须作出函数y=-x 2 -4x(x≤0)的图象关于原点对称的图象,看它与函数f(x)=log 3 x(x>0)交点个数即可.
根据题意:当x>0时,-x<0,
则f(-x)=-(-x) 2 -4(-x)=-x 2 +4x,
则函数y=-x 2 -4x(x≤0)的图象关于原点对称的函数是y=x 2 -4x(x≥0)
由题意知,作出函数y=x 2 -4x(x≥0)的图象及函数f(x)=log 3 x(x>0)的图象如下图所示
由图可得两个函数图象共有两个交点
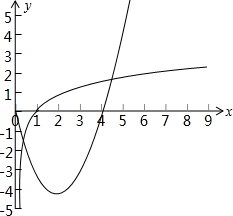
即f(x)的“友好点对”有:2个.
故答案为:2
点评:
本题主要考查了奇偶函数图象的对称性,以及数形结合的思想,解答的关键在于对“友好点对”的正确理解,合理地利用图象法解决.
分析:
根据题意:“友好点对”,可知,欲求f(x)的“友好点对”,只须作出函数y=-x 2 -4x(x≤0)的图象关于原点对称的图象,看它与函数f(x)=log 3 x(x>0)交点个数即可.
根据题意:当x>0时,-x<0,
则f(-x)=-(-x) 2 -4(-x)=-x 2 +4x,
则函数y=-x 2 -4x(x≤0)的图象关于原点对称的函数是y=x 2 -4x(x≥0)
由题意知,作出函数y=x 2 -4x(x≥0)的图象及函数f(x)=log 3 x(x>0)的图象如下图所示
由图可得两个函数图象共有两个交点

即f(x)的“友好点对”有:2个.
故答案为:2
点评:
本题主要考查了奇偶函数图象的对称性,以及数形结合的思想,解答的关键在于对“友好点对”的正确理解,合理地利用图象法解决.
看了若直角坐标平面内的两个不同点M...的网友还看了以下:
若角α与β的终边关于y轴对称,求出角α与β的关系.求你们给我详细点的过程若角α与β的终边关于y轴对 2020-05-16 …
1.若函数y=4x+b的图像与两坐标轴围成的三角形的面积是8,则函数的解析式为().2.在直角坐标 2020-06-06 …
对于一个三角形设其三个内角的度数为X、Y、Z.若x、Y、Z满足X^2+Y^2=Z^2,我们定义这个 2020-06-12 …
若A={(x,y)|(x-1)^2+(y-2)^2≤5/4}与B={(x,y)||x-1|+2|y 2020-06-14 …
(1)若角αβ的终边关于直线x+y=0对称且α=-60°则β的值是(2)设角α的终边与252°的角 2020-07-19 …
如图,Rt△AOB在直角坐标系中,OB=2,OA=4,直线y=kx(k>0)与AB交于点C,若直线 2020-07-30 …
(1)若角α与角β的终边关于y轴对称,则α与β的关系是(2)若角α与角β的终边互为反向延长线,则α 2020-07-30 …
已知角的顶点在原点,始边为X轴的非负半轴.若角终边经过P(负根号3,y)已知角x的顶点在原点,始边 2020-07-30 …
若角α的余弦线是单位长度的有向线段,那么角α的终边在()A.y轴上B.x轴上C.直线y=x上若角α 2020-08-02 …
对于一个三角形,设其三个内角的度数分别为x°、y°和z°,若x、y、z满足x2+y2=z2,我们定义 2020-11-04 …