早教吧作业答案频道 -->数学-->
已知钝角三角形ABC,点D在BC的延长线上,连接AD,若∠DAB=90°,∠ACB=2∠D,AD=2,AC=32,根据题意画出示意图,并求tanD的值.
题目详情
已知钝角三角形ABC,点D在BC的延长线上,连接AD,若∠DAB=90°,∠ACB=2∠D,AD=2,AC=
,根据题意画出示意图,并求tanD的值.
| 3 |
| 2 |
▼优质解答
答案和解析
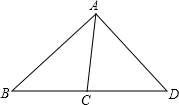 如图,∵∠ACB=∠D+∠CAD,∠ACB=2∠D,
如图,∵∠ACB=∠D+∠CAD,∠ACB=2∠D,
∴∠CAD=∠D,
∴CA=CD.
∵∠DAB=90°,
∴∠B+∠D=90°,∠BAC+∠CAD=90°,
∴∠B=∠BAC,
∴AC=CB,
∴BD=2AC=2×
=3.
在Rt△ABD中,∵∠DAB=90°,AD=2,
∴AB=
=
,
∴tanD=
=
.
 如图,∵∠ACB=∠D+∠CAD,∠ACB=2∠D,
如图,∵∠ACB=∠D+∠CAD,∠ACB=2∠D,∴∠CAD=∠D,
∴CA=CD.
∵∠DAB=90°,
∴∠B+∠D=90°,∠BAC+∠CAD=90°,
∴∠B=∠BAC,
∴AC=CB,
∴BD=2AC=2×
| 3 |
| 2 |
在Rt△ABD中,∵∠DAB=90°,AD=2,
∴AB=
| 32-22 |
| 5 |
∴tanD=
| AB |
| AD |
| ||
| 2 |
看了已知钝角三角形ABC,点D在B...的网友还看了以下:
Ⅰ.喷瓜的性别类型由AD、a+、ad三种基因决定,请根据有关信息回答下列问题:(1)AD、a+、a 2020-05-13 …
在梯形ABCD中,AD‖BC,∠A=90°,AB=7,AD=2,BC=3,问“在线段AB上是否存在 2020-05-16 …
已知△ABC ,AB=3,AC=4AD⊥BC于D,且AD=2,求三角形ABC外接圆的面积. 速求啊 2020-05-16 …
2.A“三”这个数字在我国的传统文化中具有特殊的意义,《庄子》有言:“道生一,一生二二生三,三生万 2020-05-17 …
己知三角形ABC,1)画BC边上的中线AD.2)画三角形ABD的角平分线.AE.3)画三角形ADC 2020-07-08 …
设abc满足a+b+c=1,a方+b方+c方=2,a三方+b三方+c三方=3求(1)abc的值(2 2020-07-22 …
[1]9a二次方-13.[2]a三次方-8a 2020-07-31 …
设AD是三角形ABC的中线,利用余弦定理证明AD^2=(B^2+C^2-a^2/2)/2若ABC的 2020-08-02 …
函数题,A是不是B的函数(1)A等边三角形的面积B等边三角形的边长这两者是不是函数关系,A是不是B 2020-08-03 …
紧急!A+B+C=1,A平方+B平方+C平方=2,A三方+B三方+C三方=3,问A四方+B四方+C四 2020-11-07 …