早教吧作业答案频道 -->数学-->
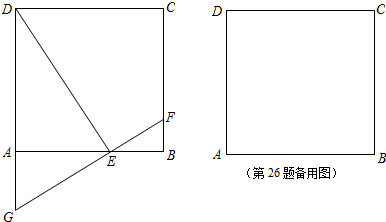
如图,在正方形ABCD中,点E在边AB上(点E与点A、B不重合),过点E作FG⊥DE,FG与边BC相交于点F,与边DA的延长线相交于点G.(1)猜想BF、AG、AE的数量关系,并证明你所得到的结论;(2)如果
题目详情
如图,在正方形ABCD中,点E在边AB上(点E与点A、B不重合),过点E作FG⊥DE,FG与边BC相交于点F,与边DA的延长线相交于点G.
(1)猜想BF、AG、AE的数量关系,并证明你所得到的结论;
(2)如果正方形的边长为2,FG的长为
,求点A 到直线DE的距离.
(1)猜想BF、AG、AE的数量关系,并证明你所得到的结论;
(2)如果正方形的边长为2,FG的长为
| 2 |
| 5 |

▼优质解答
答案和解析
(1)BF+AG=AE.理由如下: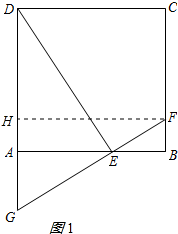
过点F作FH⊥DA,垂足为H,如图所示:
∵在正方形ABCD中,∠DAE=∠B=90°,
∴四边形ABFH是矩形,
∴FH=AB=DA.
∵BD⊥FG,
∴∠G=90°-∠ADE=∠DEA.
在△FHG和△DAE中,
,
∴△FHG≌△DAE(AAS).
∴GH=AE,即HA+AG=AE.
∵BF=HA,
∴BF+AG=AE.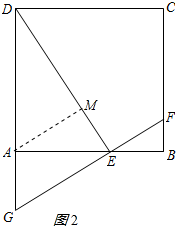
(2)过点A作AM⊥DE垂足为M.如图2所示:
由(1)得:△FHG≌△DAE,
∴DE=FG=
在Rt△ADE中,AE=
=
=
,
∵AE•AD=DE•AM,
∴AM=
=
即点A到直线DE的距离是
.

过点F作FH⊥DA,垂足为H,如图所示:
∵在正方形ABCD中,∠DAE=∠B=90°,
∴四边形ABFH是矩形,
∴FH=AB=DA.
∵BD⊥FG,
∴∠G=90°-∠ADE=∠DEA.
在△FHG和△DAE中,
|
∴△FHG≌△DAE(AAS).
∴GH=AE,即HA+AG=AE.
∵BF=HA,
∴BF+AG=AE.

(2)过点A作AM⊥DE垂足为M.如图2所示:
由(1)得:△FHG≌△DAE,
∴DE=FG=
| 5 |
| 2 |
在Rt△ADE中,AE=
| DE2-AD2 |
(
|
| 3 |
| 2 |
∵AE•AD=DE•AM,
∴AM=
| AE•AD |
| DE |
| 6 |
| 5 |
即点A到直线DE的距离是
| 6 |
| 5 |
看了如图,在正方形ABCD中,点E...的网友还看了以下:
已知等边三角形abc的边上为a.则它一边上的高是多少?面积多少? 2020-06-05 …
如图,在一个规格为4×8的球台上,有两个小球P和Q,若击打小球P经过球台的边AB反弹后,恰好击中小 2020-07-05 …
有一条可坐20人的木船,要载40名学生从湖边到湖中A、B两岛参观,从湖边驶到A岛需要10分钟,到B 2020-07-11 …
如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停 2020-07-19 …
一个正方形花坛,每条边上摆上4盆花,四周一共需要多少盆花?如果每条边上摆a盆花,四周一共需要盆 2020-07-28 …
勾股定理超难的题十级以上再进吧!将直角三角形ABC绕直角顶点C旋转,使点A落在BC边上的A',利用 2020-07-29 …
在矩形ABCD中AB=3,AD=5使点a落在BC边上的A’处,折痕为P,Q.当点A’在BC边上移动 2020-07-30 …
如图,将半径为1的圆的边上的A点与数轴的原点重合,然后沿着数轴向右滚动,滚动一周得到点A′,则点A′ 2020-11-17 …
湖边上有A,B两个村庄(如图),从A到B有两条路可走,即A→P→B和A→Q→B.试判别哪条路更短,并 2020-11-22 …
在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ 2020-11-28 …