早教吧作业答案频道 -->数学-->
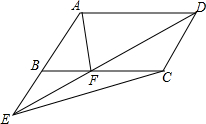
如图所示，E是▱ABCD的边AB延长线上一点，DE交BC于F，求证：S△ABF=S△EFC．
题目详情
如图所示，E是▱ABCD的边AB延长线上一点，DE交BC于F，求证：S△ABF=S△EFC．
▼优质解答
答案和解析
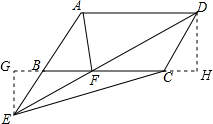如图，分别过点E、D作EG⊥BC、DH⊥BC，交直线BC于G、H．
∵四边形ABCD是平行四边形，
∴BE∥CD，
∴△BEF∽△CDF，
∴
=
，即BF•DH=CF•EG，
∵S△ABF=
BF•DH，S△EFC=
CF•EG，
∴S△ABF=S△EFC．
如图，分别过点E、D作EG⊥BC、DH⊥BC，交直线BC于G、H．∵四边形ABCD是平行四边形，
∴BE∥CD，
∴△BEF∽△CDF，
∴
| BF |
| CF |
| EG |
| DH |
∵S△ABF=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABF=S△EFC．
看了如图所示，E是▱ABCD的边A...的网友还看了以下：
1.a≠0,b≠0,则a/|a|＋b/|b|的不同取值的个数为（）A.3B.2C.1D.02.若|x 2020-03-31 …
读下图，据此回答1-3题：1.四幅图中位在亚洲与北美洲边界的图是：A.a图B.b图C.c图D.d图 2020-05-02 …
基本不等式超费解130已知a>b>0,求a2+1/（a*b)+1/[a*(a-b)]的最小值.a2 2020-05-13 …
已知f(x)是R上的减函数,a为常数,a∈R,则f(3/2)与f(a²+a+2)的大小关系是--- 2020-05-13 …
已知函数f(x)=(a*2^x+a2-2)÷(2^x-1)(x∈R,x≠0),其中a为常数,且a﹤ 2020-05-13 …
设集合A={1,a,b},B={a,a^2,ab}且A=B,求实数A,B的值因为集合需要满足互异性 2020-05-15 …
求证：函数y=f(a+x)与函数y=f(a-x)关于x=0对称,其中x∈R求证：函数y=f(a+x 2020-05-16 …
命题1.若f(x-a)=f(a-x)则函数f(x)的图像关于y轴对称2.函数y=f(x-a)与函数 2020-06-04 …
关于函数f(x)在图像上的平移1.f（x）在图像上怎么平移得到f(x+1)2.f（x）在图像上怎么 2020-06-05 …
假设集合A满足以下条件：诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …