早教吧作业答案频道 -->数学-->
如图,一次函数y=-23x+b的图象与x轴、y轴分别交于点A、B,线段AB的中点为D(3,2).将△AOB沿直线CD折叠,使点A与点B重合,直线CD与x轴交于点C.(1)求此一次函数的解析式;(2)求点C的
题目详情
如图,一次函数y=-
x+b的图象与x轴、y轴分别交于点A、B,线段AB的中点为D(3,2).将△AOB沿直线CD折叠,使点A与点B重合,直线CD与x轴交于点C.
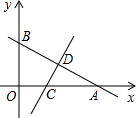
(1)求此一次函数的解析式;
(2)求点C的坐标;
(3)在坐标平面内存在点P(除点C外),使得以A、D、P为顶点的三角形与△ACD全等,请直接写出点P的坐标.
| 2 |
| 3 |

(1)求此一次函数的解析式;
(2)求点C的坐标;
(3)在坐标平面内存在点P(除点C外),使得以A、D、P为顶点的三角形与△ACD全等,请直接写出点P的坐标.
▼优质解答
答案和解析
(1)设A点坐标为(a,0),B点坐标为(0,b),
由线段AB的中点为D(3,2),得
=3,
=2,
解得a=6,b=4.
即A(6,0),B(0,4)
(2)如图1: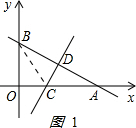 连接BC,设OC=x,则AC=CB=6-x,
连接BC,设OC=x,则AC=CB=6-x,
∵∠BOA=90°,
∴OB2+OC2=CB2,
42+x2=(6-x)2,
解得x=
,
即C(
,0);
(3)①当△ACD≌△APD时,设P1(c,d),
由D是PC的中点,得
=3,
=2,
解得c=
,d=4,
即P1(
,4);
如图2: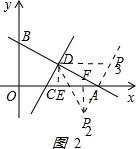 ,
,
②当△ACD≌△DP2A时,
做DE⊥AC与E,P2F⊥AC与F点,DE=2,CE=3-
=
,
由△CDE≌△AP2F,
AF=CE=
,P2F=DE=2,
OF=6-
=
,
∴P2(
,-2);
③当△ACD≌△DP3A时,设P3(e,f)
A是线段P2P3的中点,得
=6,
=0,
解得e=
,f=2,
即P3(
,2),
综上所述:P1(
,4);P2(
,-2);P3(
,2).
由线段AB的中点为D(3,2),得
| 0+a |
| 2 |
| 0+b |
| 2 |
解得a=6,b=4.
即A(6,0),B(0,4)
(2)如图1:
 连接BC,设OC=x,则AC=CB=6-x,
连接BC,设OC=x,则AC=CB=6-x,∵∠BOA=90°,
∴OB2+OC2=CB2,
42+x2=(6-x)2,
解得x=
| 5 |
| 3 |
即C(
| 5 |
| 3 |
(3)①当△ACD≌△APD时,设P1(c,d),
由D是PC的中点,得
c+
| ||
| 2 |
| d+0 |
| 2 |
解得c=
| 13 |
| 3 |
即P1(
| 13 |
| 3 |
如图2:
 ,
,②当△ACD≌△DP2A时,
做DE⊥AC与E,P2F⊥AC与F点,DE=2,CE=3-
| 5 |
| 3 |
| 4 |
| 3 |
由△CDE≌△AP2F,
AF=CE=
| 4 |
| 3 |
OF=6-
| 4 |
| 3 |
| 14 |
| 3 |
∴P2(
| 14 |
| 3 |
③当△ACD≌△DP3A时,设P3(e,f)
A是线段P2P3的中点,得
e+
| ||
| 2 |
| f+(-2) |
| 2 |
解得e=
| 22 |
| 3 |
即P3(
| 22 |
| 3 |
综上所述:P1(
| 13 |
| 3 |
| 14 |
| 3 |
| 22 |
| 3 |
看了如图,一次函数y=-23x+b...的网友还看了以下:
因式分解a(x一y)一b(y一x)+(x一y)c 2020-04-05 …
已知丨x-4丨十y^2一2y十1=0,求[(x十y)^2一(x一y)^2]/2xy的值 2020-04-27 …
计算[4(x十y)的平方一x一y]除以(x十y)十(3一3.14x3)的0次方= 2020-05-13 …
某同学把7x(囗—3)错抄写为7X囗一3,抄错后计算得到的答案为y.若正确答案为x,某同学把7x( 2020-05-16 …
一5(x一y一Z)一2(x一2Y+3z)2(x一2y+一5(x一y一Z)一2(x一2Y+3z)2( 2020-06-06 …
折线统计图X轴Y轴如何共用原点.也就是X轴的起始数据0和Y轴的0在一个点上 2020-06-06 …
根号3x十y一z一2加根号2x十y一z等于根号x十y一2002加上根号2002一x一y:求x.y. 2020-06-12 …
已知X的平方一y的平方=20,求[(X一y)的平方十4Xy][(X十y)的平方一4Xy]的值. 2020-06-12 …
x十y=73,x一y=35,x等于多少,y等于多少? 2020-07-17 …
x十y=242,x一y=39,x=?y=? 2020-07-19 …