早教吧作业答案频道 -->数学-->
如图,己知AB是半径为2的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形.(1)求证:△DFB是等腰三角形;(2)若AF=1,求DA的长度;(3)若DA=7AF,
题目详情
如图,己知AB是半径为2的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形.
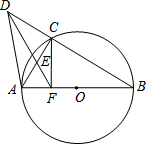
(1)求证:△DFB是等腰三角形;
(2)若AF=1,求DA的长度;
(3)若DA=
AF,求证:CF⊥AB.

(1)求证:△DFB是等腰三角形;
(2)若AF=1,求DA的长度;
(3)若DA=
| 7 |
▼优质解答
答案和解析
(1)证明:∵AB是 O直径,
∴∠ACB=90°,
∵△AEF为等边三角形,
∴∠CAB=∠EFA=60°
∴∠B=30°,
∵∠EFA=∠B+∠FDB,
∴∠B=∠FDB=30°,
∴△DFB是等腰三角形;
(2) 过点A作AM⊥DF于点M,
∵AB=2×2=4,AF=1,
∴BF=4-1=3,
∵DF=BF,
∴DF=3,
∵△AEF是等边三角形,
∴FM=EM=
AF=
,AM=
FM=
,
在Rt△DAM中,AD=
AF=
×1=
;
(3)证明:设AF=2a,
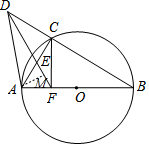
∵△AEF是等边三角形,
∴FM=EM=a,AM=
a,
在Rt△DAM中,AD=
AF=2
a,AM=
a,
∴DM=5a,∴DF=BF=6a,
∴AB=AF+BF=8a,
在Rt△ABC中,∠B=30°,∠ACB=90°,
∴AC=4a,
∵AE=EF=AF=2a,
∴CE=AC-AE=2a,
∴∠ECF=∠EFC,
∵∠AEF=∠ECF+∠EFC=60°,
∴∠CFE=30°,
∴∠AFC=∠AFE+∠EFC=60°+30°=90°,
∴CF⊥AB.
∴∠ACB=90°,
∵△AEF为等边三角形,
∴∠CAB=∠EFA=60°
∴∠B=30°,
∵∠EFA=∠B+∠FDB,
∴∠B=∠FDB=30°,
∴△DFB是等腰三角形;
(2) 过点A作AM⊥DF于点M,
∵AB=2×2=4,AF=1,
∴BF=4-1=3,
∵DF=BF,
∴DF=3,
∵△AEF是等边三角形,
∴FM=EM=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
在Rt△DAM中,AD=
| 7 |
| 7 |
| 7 |
(3)证明:设AF=2a,

∵△AEF是等边三角形,
∴FM=EM=a,AM=
| 3 |
在Rt△DAM中,AD=
| 7 |
| 7 |
| 3 |
∴DM=5a,∴DF=BF=6a,
∴AB=AF+BF=8a,
在Rt△ABC中,∠B=30°,∠ACB=90°,
∴AC=4a,
∵AE=EF=AF=2a,
∴CE=AC-AE=2a,
∴∠ECF=∠EFC,
∵∠AEF=∠ECF+∠EFC=60°,
∴∠CFE=30°,
∴∠AFC=∠AFE+∠EFC=60°+30°=90°,
∴CF⊥AB.
看了如图,己知AB是半径为2的圆O...的网友还看了以下:
al离子与f离子生成络合物?为什么题目说他们双水解选择项al的氯化物水溶液中滴加过量f与na形成的 2020-04-11 …
19、(2009•梅州)如图,矩形ABCD中,AB=5,AD=3.点E是CD上的动点,以AE为直径 2020-05-24 …
f(x)是定义在R上的函数,且对任意实数x,y都有f(x+y)=f(x)+f(y)-1成立,当f( 2020-06-02 …
定义在R上的函数y=f(x),满足f(x+2)=-1/f(x),则().A.f(x)不是周期函数B 2020-06-03 …
f(x)是R上的函数,若f(x+1)和f(x-1)都是奇函数,则下列判断正确的是1、f(x)是偶函 2020-06-08 …
设f(x)是连续函数,F(x)是f(x)的原函数,则下列结论正确的是?A当f(x)是奇函数时,F( 2020-07-30 …
在等边△ABC中,AB=2,点P为AB边上任一点,过点P作PE垂直BC于E,过E作EF垂直AC于F 2020-07-30 …
设f(x)在x=0的某邻域内存在二阶导数,且f'(x)=0,lim(x→0)f''(x)/|x|= 2020-07-31 …
1.函数f(x)是定义在R上的偶函数,当x∈(0,+∞)时,f(x)=lg(x+1),那么当x∈( 2020-07-31 …
英朗GT空调温度后面怎么是F?打个比方说30℃才对可现在是30°F这是什么意思?英朗GT空调温度后面 2020-11-05 …