早教吧作业答案频道 -->数学-->
如图,在△ABC中,AD为∠BAC的平分线,点E在BC的延长线上,且∠EAC=∠B,以DE为直径的半圆交AD于点F,交AE于点M.(1)判断AF与DF的数量关系,并说明理由.(2)只用无刻度的直尺画出△ADE的
题目详情
如图,在△ABC中,AD为∠BAC的平分线,点E在BC的延长线上,且∠EAC=∠B,以DE为直径的半圆交AD于点F,交AE于点M.
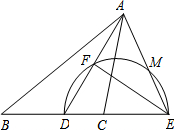
(1)判断AF与DF的数量关系,并说明理由.
(2)只用无刻度的直尺画出△ADE的边DE上的高AH(不要求写作法,保留作图痕迹).
(3)若EF=8,DF=6,求DH的长.

(1)判断AF与DF的数量关系,并说明理由.
(2)只用无刻度的直尺画出△ADE的边DE上的高AH(不要求写作法,保留作图痕迹).
(3)若EF=8,DF=6,求DH的长.
▼优质解答
答案和解析
(1)AF=DF,
理由如下:
∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵∠B=∠CAE,
∴∠BAD+∠B=∠CAD+∠CAE.
即∠ADE=∠DAE,
∴AE=DE,
∵DE是直径,
∴EF⊥AD,
∴AF=DF;
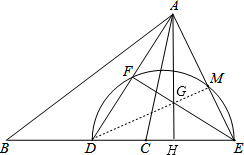 (2)如图:连接DM,DM交EF于G,作射线AG交DE于H,此时AH是高.
(2)如图:连接DM,DM交EF于G,作射线AG交DE于H,此时AH是高.
(3)在△EFD中,EF=8,DF=6,由勾股定理得,DE=AE=10,
∵AH是DE边上的高,
∴∠AHD=90°,
∵∠EFD=90°,
∴∠AHD=∠EFD,
∵∠ADH=∠EDF,
∴△ADH∽△EDF,
∴
=
,
∴
=
,
解得DH=
.
理由如下:
∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵∠B=∠CAE,
∴∠BAD+∠B=∠CAD+∠CAE.
即∠ADE=∠DAE,
∴AE=DE,
∵DE是直径,
∴EF⊥AD,
∴AF=DF;
 (2)如图:连接DM,DM交EF于G,作射线AG交DE于H,此时AH是高.
(2)如图:连接DM,DM交EF于G,作射线AG交DE于H,此时AH是高.(3)在△EFD中,EF=8,DF=6,由勾股定理得,DE=AE=10,
∵AH是DE边上的高,
∴∠AHD=90°,
∵∠EFD=90°,
∴∠AHD=∠EFD,
∵∠ADH=∠EDF,
∴△ADH∽△EDF,
∴
| DH |
| DF |
| AD |
| DE |
∴
| DH |
| 6 |
| 12 |
| 10 |
解得DH=
| 36 |
| 5 |
看了如图,在△ABC中,AD为∠B...的网友还看了以下:
a为有理数,化简a-5/|a-5| (a不等于5).具体解题思路 2020-04-06 …
数学题关于有理数的若a为有理数,在-a与a之间(不含-a与a)有1997个整数,则a的取值范围是什 2020-04-08 …
设a为有理数,x为无理数,证明:(1)a+x是无理数;(2)当a≠0时,ax是无理数. 2020-05-13 …
下列语句中正确的是()A.若a为有理数,则必有|a|-a=0B.两个有理数的差小于被减数C.两个有 2020-05-13 …
a为有理数那么3+a一定大于3-a吗?为什么?还有一个问题,整数23读作“二十三”应是2x10+3 2020-05-13 …
一个挺难的数学题√a(a为正整数)有时为有理数,比如a=4,9.但有时√a又为无理数,比如a=5, 2020-05-20 …
计算机用于管理系统的发展的各个阶段中,事务处理阶段的主要目的之一是()。A.为管理人员提供优越的 2020-05-24 …
若a为有理数,则-a与|a|的和是()若a为有理数,则-a与|a|的和是(B)A.可能是负数B.不 2020-06-03 …
设A为有理数,B为无理数,如何证明A+B为无理数,以及当A不等于0时AB为无理数? 2020-06-14 …
如果一个数x与2相乘的结果是有理数,则这个数x的一般形式x=2a(a为有理数)或x=a2(a为有理数 2020-11-06 …